Magnetic Dipole : Magnetic Dipole Moment and Properties
A magnetic dipole is a system, that when placed in a magnetic field, exerts a force on it, which tends to rotate the system in such a way that its axis becomes parallel to the magnetic field. Molecules, atoms and basic particles of magnetic substances are also magnetic dipoles.
There is an important difference between a magnetic dipole and an electric dipole. In an electric dipole, two equal, but opposite types of point charges are located at a short distance from each other.
Both these charges have their own independent existence and can be separated from each other.
Thus, a single electric charge is the simplest electric structure. In magnetic dipole the situation is completely different. The magnetic dipole itself is the simplest magnetic structure because a single magnetic pole does not exist. Although two poles are imagined in each magnetic dipole, they can never be separated.
Moment of Couple on a Magnetic dipole due to an external magnetic Field
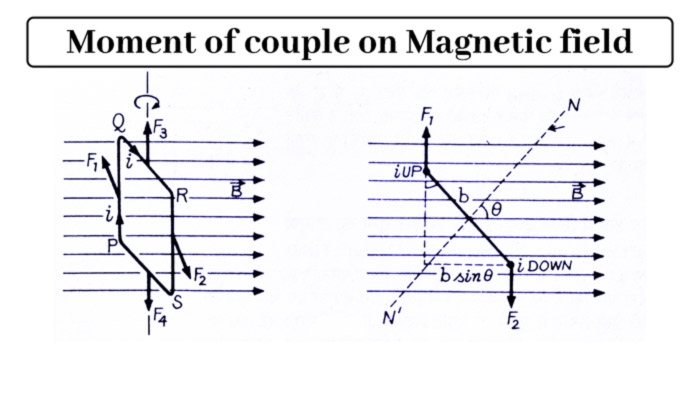
Suppose a rectangular loop PQRS is suspended in a uniform external magnetic field B. Length of the loop is PQ = RS = l and breadth QR = SP = b.
Let the current i flow in the loop. We know that a current carrying current in a magnetic field experiences a conducting force.
Therefore, a force is exerted on each arm of the current loop, whose direction is according to the law of right hand palm. The vertical sides PQ and RS of the current loop, each of length l, are always perpendicular to the magnetic field B.
Hence the force on them
F1 = F2 = ilB
Forces F1 and F2 are equal, parallel and opposite, but their lines of action are different. Therefore, they create a force which is called deflecting couple. Due to this force the loop starts rotating from its position.

Let the axis of the moment loop make an angle θ with the direction of the magnetic field B. Then the moment of deflection couple at this moment
τ = Force F1 (= F2) x perpendicular length
= ilB x b sinθ
but l x b = A(area of loop)
τ = iAB sinθ
The forces F3 and F4 acting on the remaining two sides of the loop QR and SP are equal and opposite to each other and they have the same line of action.
So these two forces cancel each other. Thus the net force on the current loop is zero, but a force couple appears on it, whose moment is τ = iAB sinθ. This couple force causes the current to rotate the loop to such a position that the NN` of the loop is parallel to the magnetic field B. In this case (θ = 0) the zero of the force couple becomes zero.
The formula for the moment of force couple τ = iAB sinθ is true for a closed loop of any size. This is because we can consider any loop L to be divided into very small adjacent rectangular loops.
The same current (i) is flowing in clockwise direction in each small loop. If we look at a small loop A, then the magnetic effect of the current flowing in any of its arms is canceled by the magnetic effect of the equal and opposite current flowing in its adjacent loop.
The same action happens in all the loops. The magnetic effect of the current (i) flowing in only those arms of the loops is not canceled which coincides with the boundary of the larger loop L. So the resultant magnetic effect of all the smaller loops is the same as that of the larger loop L.
If instead of one loop, there is a coil or solenoid made of several loops, then the half of the above force couple will be τ = iAB sinθ on each loop. Hence the torque of the pair of forces acting on the whole coil.

τ = NiAB sinθ
Where N is the number of loops in the coil.
If the coil is in a radial magnetic field, then the plane of the coil is parallel to the lines of force in each case i.e. θ = 90 in each case. Hence, in this case the torque of the pair of forces acting on the coil
Magnetic Dipole Moment :
When a magnetic dipole is placed in a magnetic field, a couple acts on it which tries to make the axis of torque parallel to the magnetic field.
Let the magnetic dipole be placed in a uniform magnetic field B making an angle θ with the direction of the field. Then the torque of the pair of forces acting on the dipole –
τ = M B sinθ
Where M is the torque of the magnetic dipole. If the axis of the magnetic dipole is perpendicular to the magnetic field B (θ = 90°), then the force moment on it will be maximum τmax.
τmax = M B,
M = τmax / B
If B = 1 , then M = τmax
Therefore, the magnetic moment of a magnetic dipole is the force moment that is exerted on the dipole when this dipole is kept perpendicular to the direction of the field in a unit and uniform magnetic field.
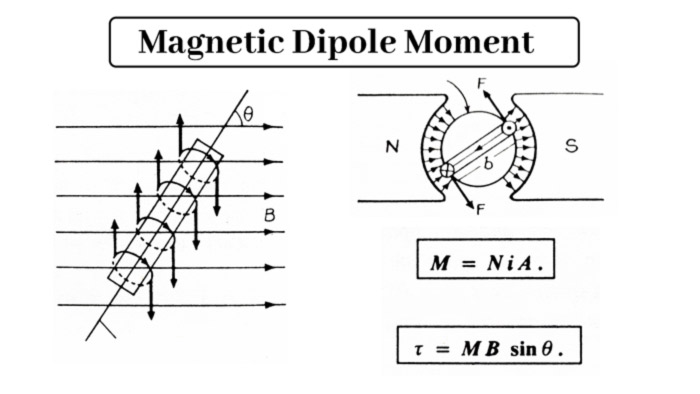
The magnetic dipole moment is a scalar quantity and it is along the axis of the dipole. The direction of the magnetic moment of the current loop is determined by the right hand rule. If we spread the claw of our right hand completely and bend the fingers around the loop in the direction of the current, then the thumb will be towards the direction of the magnetic moment.
Magnetic Moment (M) = empere – meter2
Dimensions of Magnetic Moment – [L2A]
Magnetic Field due to a magnetic dipole
End on position :- If the magnetic moment (M) of a magnetic dipole or small bar-magnet is M, then the magnetic field at a point P in vacuum at a distance of r meter from its midpoint on its axial line.
B = (μ0 / 4π) x (2M / r3) Newton / ampere-meter
B = 10-7 (2M / r3) Newton / ampere-meter
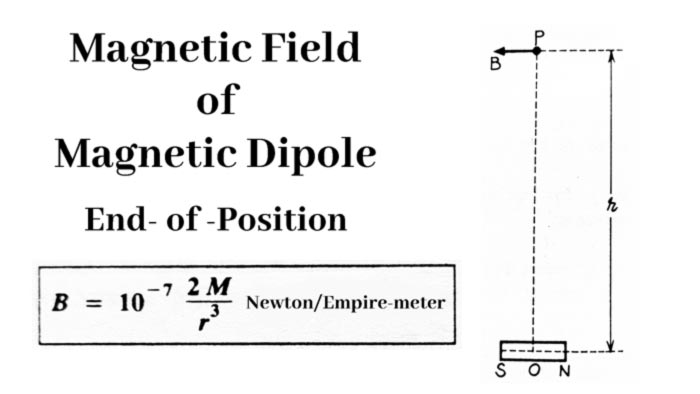
The magnetic field B is directed parallel to the magnetic axis from the south pole S to the north pole N.
Broad side on position :- magnetic field at a point P in the air at a distance of r meter from the center of the magnet on its neutral line due to a magnetic dipole or small bar magnet
B = 10-7 (M / r3) Newton / ampere-meter

The magnetic field B is directed from the north pole N to the south pole S, parallel to the axis of the magnet.