Rigid Body: Moment of Force or Torque formula
Rigid Body
If the particles of the body do not have any displacement relative to each other by applying an external force on a body, then such a body is called a ‘rigid body’.
In reality, no body is completely rigid, but generally in solid bodies (except rubber etc.), the relative displacement caused by the external force is so small that it can be neglected. In common parlance, the meaning of the body is from the firm body.
Moment of Force or torque
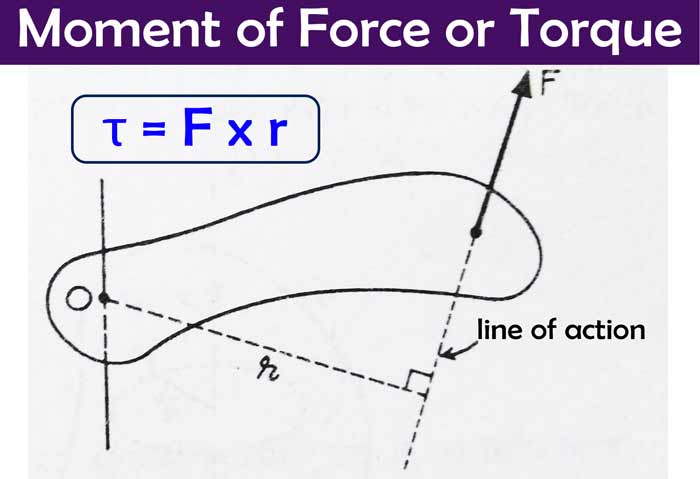
When an external force acting on a body tends to rotate that body about an axis, then this tendency is called Moment of Force or torque. The rotation of a force about the axis of rotation is equal to the product of the magnitude of the moment of force and the perpendicular distance of the line of action of the force from the axis of rotation.
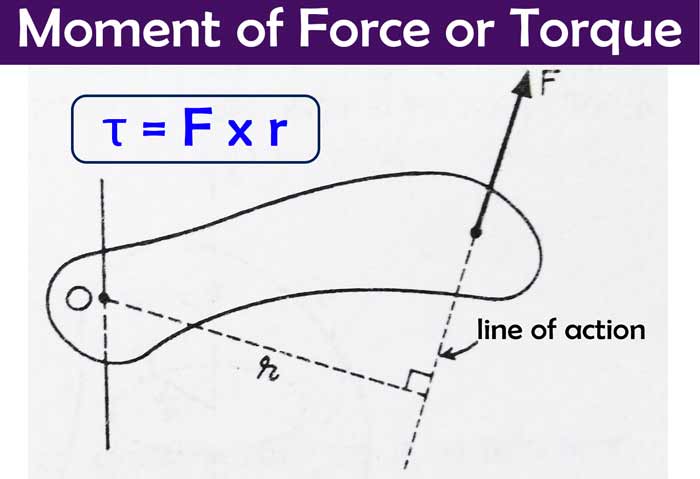
In the figure, a body is free to rotate about an axis passing through point O and perpendicular to the plane of the paper. When a force F is applied on the body to the plane of the paper, the body starts rotating about this axis.
If r is the perpendicular distance of the line of action of the force from the point O, then the rotation of the force f about the axis is the moment-
moment of force formula : τ = F x r
If the force tends to rotate the body anticlockwise, then the torque is said to be positive, and if it tends to rotate the body clockwise, then the torque is said to be negative. The unit of moment of force is ‘Newton-meter‘ and the dimension formula (ML2T-2 ).
If the force tends to rotate the body anticlockwise, then the torque is said to be positive, and if it tends to rotate the body clockwise, then the torque is said to be negative. The unit of moment of force is ‘Newton-meter‘ and the dimension formula (ML2T-2 ).
It is clear from the above formula that if the value of r is zero, that is, the line of action of the force passes through the point O, then the moment of force will be zero. In this state the force will not be able to rotate the body about O no matter how much it is in magnitude.
Conversely, the farther the line of action of the force is from the point O, the greater the moment of the force about the point O, or the less force is required to rotate the body.
This fact is used in daily life, such as the handle that turns the flour mill of households is ‘away’ from the spike, the handle is ‘long’ in the hand drawn water taps, and the handles on the doors. ‘Away’ from possession. The handle of the screwdriver is also made ‘wide’ for this reason.
General Motion of a Rigid Body
There are generally two types of motion of a rigid body: translational motion and rotational motion.
Translational Motion
When a body moves in such a way that each of its particles is displaced in the same direction by the same distance in a given time interval, then its motion is called ‘translational motion‘.
In the figure, the translational motion of a body, inertial reference frame with respect to X,Y,Z from position A to B and from B to C is shown. In each case, the axes of a reference system (X,Y,Z) bound to the body are parallel to the axes of the observer’s system of reference (X,Y,Z).
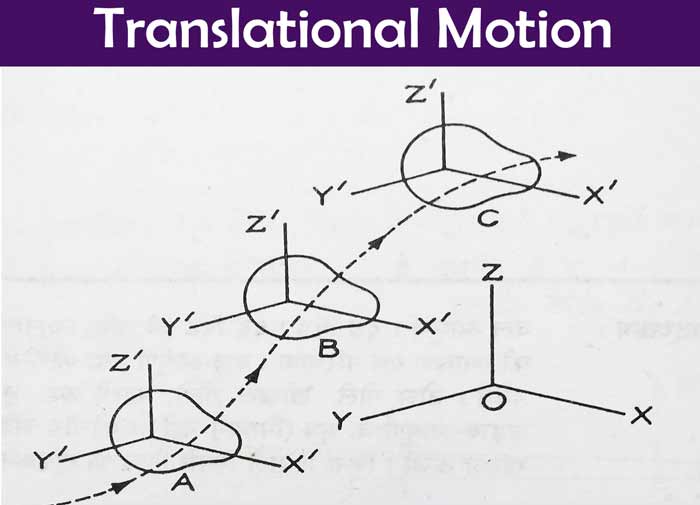
Here there are 3 degrees of translational freedom, that is, 3 variables will be required to express the position of the body relative to the reference system.
Since the displacement of any particle of the body is the same as that of any other particle, we can represent the motion of the whole body by the motion of a single particle (such as the center of mass of the body).
Apart from this, we can also assume that the entire mass M of the body is concentrated at the center of mass of the body and the resultant F of all the external forces acting on the body is acting on the center of mass of the body. Then, the acceleration of the center of mass –
acm = F/M
Translational Motion
When a body moves about a fixed axis in such a way that every particle of the body is moving on a circular path and the centers of all the circles are on that axis, then its motion is called ‘rotational motion‘, and that axis is called axis of rotation.
The particles which are on the axis of rotation remain stationary, so they are not considered. Figure shows the rotational motion of a body about a fixed-axis OZ.
Any particle of a body, such as P whose position vector is r, moves in a circle whose center is on the axis of rotation. There are 3 degrees of rotational freedom, that is, 3 angles will be required to express the orientation of the body relative to the reference system.

The general motion (translational + rotation) of the body is shown in Figure. In this, the reference system (X,Y,Z) attached to the body rotates continuously with respect to the observer’s reference system (X,Y,Z).
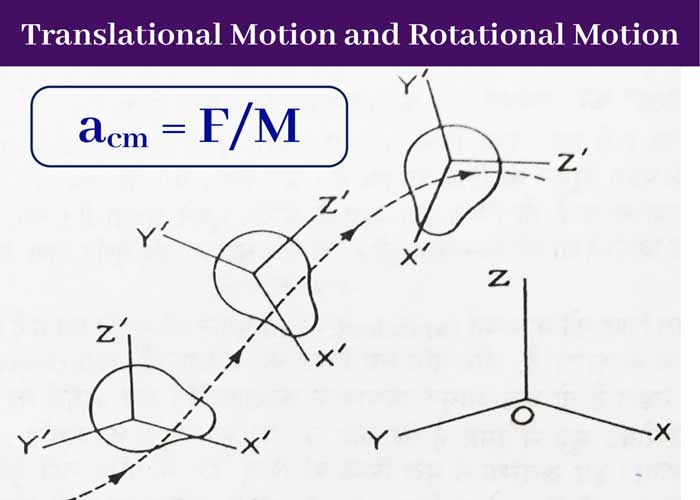
Obviously, to find the position and orientation of the body relative to the reference system (X, Y, Z), 6 instructions will be required, in which 3 translational directions for any point of the body are X, Y, Z, and 3 rotations. The directions will be angles.