Article Topics
Before studying optical isomerism, it is necessary to understand the meaning of Plane Polarised light, optical activity, specific rotation.
Plane Polarised Light
Theory of propogation of light, when rays of light move from one place to another, an imaginary medium vibrates into the particles of ether. This vibration occurs in all planes in the right-angled direction of the path of propagation of ordinary light beam.
Super trick to determine R and S configuration
Super trick to determine R and S configuration in any optical active compound: Optical Isomerism.
If the ordinary beam of light passes through the nicol prism, the ether particles vibrate in only one plane in the right-angled direction in the path of propagation of the ray of light emanating from the nicol prism.
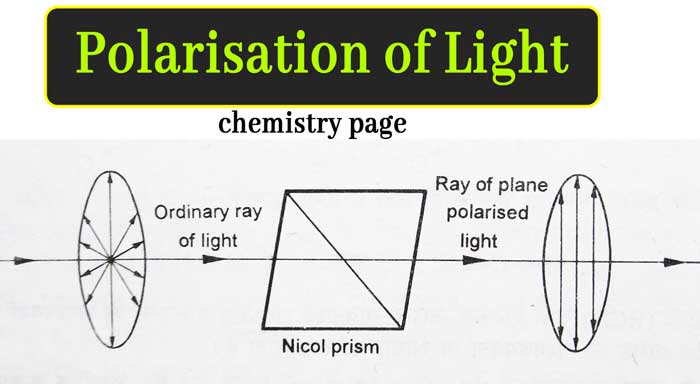
This type of light, whose imaginary medium in the path of propagation of rays, vibrates the particles of the ether in only one plane in a right-angled direction, is called plane polarized light. The equipment used to obtain plane polarized light from ordinary light is called Polariser. Hence Nicol prism is a polariser.
Optical Activity
Some substances are such that when they or their solutions are placed in the path of the plane polarized light, the bottom of the polarized light rotates to the left or to the right. This phenomenon is called optical rotation.
Such substances are called optically active substances. This property of substances is called optical activity.
At what angle does the plane of the plane polarized light rotate, it is called angle of optical rotation. If a substance or its solution rotates the plane of polarized light to the right (clockwise) then this substance is called dextrorotatory substance and if it rotates anticlockwise to the left it is called leavorotatory substance.
If a substance or its solution has no effect on the plane of the plane polarized light, then that substance is called optically inactive.
Specific Rotation
The angle at which the plane of polarized light rotates when a solution containing a gram per ml concentration of a substance is placed in a decimeter long tube and passes the plane of polarized light is called the specific rotation of that substance.
Specific rotation is often measured with the help of a D line of sodium light at 25°C. The device used for this is called polarimeter. If the amount of that substance in a 100 ml solution is c gram, the angle of optical rotation is observed by placing the solution in a l decimeter long tube and the angle of optical rotation is αobserved.
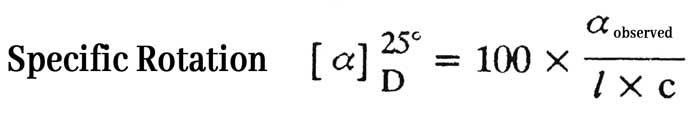
If optical rotation is clockwise, ‘+’ sign with specific rotation is used. If optical rotation is anticlockwise, the ‘-‘ sign with specific specific rotation is used.
Example: The specific optical rotation of a substance is + 52°, this implies that when a solution with a gram per ml concentration is placed in a 1 decimeter long tube at 25°C, the plane of the plane polarized sodium light rotates at an angle of 52° to the right.
Reason of Optical Activity
The properties of optical activity were first found in quartz , sodium chlorate, potassium bromate, iodate on sodium and some other inorganic substances.
Optical activity of these materials is due to the asymmetry of their crystal structure. The size of their crystals is destroyed by smelting them or dissolving them in a solvent and due to this their optical activity is also eliminated.
single crystals of benzyl[C6H5COCOC6H5] and some other carbonic compounds also exhibit optical activity due to asymmetry of the crystal structure.
Read More Articles
- Metallurgy Process | Definition with Examples
- How to compose Cement? Cement Uses.
- What is the use of plaster of Paris?
- What is the formula of sodium thiosulphate?
- Method of Preparation of Microcosmic Salt
- What is sodium carbonate used for? Sodium carbonate properties
- Sodium Hydroxide (Caustic Soda) NaOH
- How to make Hydrogen peroxide?
- What is heavy water used for?
- Isotopes of Hydrogen: Deuterium
- What is sodium carbonate used for? Sodium carbonate properties
In 1815 Jean-Baptiste Biot observed that some carbonic compounds exhibit optical activity even in the state of liquids or solutions. A detailed study of the configurations of these compounds makes it known –
Asymmetric Molecules
They are optical rotation whose molecules are asymmetric. Asymmetric molecules are also called dissymmetric molecules.
The molecule is called asymmetric molecule whose mirror image cannot be superimpose on it. Planar molecules are symmetric because all these atoms are in the same plane and their mirror images can be superimposed on them easily. Only three dimensional molecules can be asymmetric.
Optical Activity and Plane of Symmetry Chirality
How to find Optical activity, Plane of symmetry and Chirality in any compound in hindi: Stereoisomer
The molecule is called asymmetric molecule whose mirror image cannot be superimpose on it. Planar molecules are symmetric because all these atoms are in the same plane and their mirror images can be superimposed on them easily. Only three dimensional molecules can be asymmetric.
Enantiomer
The mirror images are called enantiomer of each other. The pair of molecules that are image forms of each other is called enantiomeric pair. Optical activities of enantiomers are equal in magnitude but opposite in direction.
The mirror image relationship can be explained by example of right and left hand. The right and left hands are mirror images of each other. They cannot be superimpose on each other. Hence, human hand is asymmetric. It is necessary to note here that the hand is three dimensional and while superimpose, the palm of one hand will be placed on the surface of two other hands.
Chiral
Asymmetric molecules are also called chiral (left handed or right handed). The asymmetric of molecules is also called chirality (handedness). The center or atom present in an asymmetric molecule due to the presence of which that molecule is asymmetric is called chiral center or chiral atom.
Optical Isomerism
When molecular formula, structural formula and almost all physical and chemical properties of two or more compounds are similar but their behaviour towards plane polarized light is different, they are called optical isomer of each other and this phenomenon is called optical isomerism.
Example: d-lactic acid and l-lactic acid are two compounds. They have molecular formula (C3H6O3), structure formula [CH3.CH(OH).COOH] and almost all physical and chemical properties but their specific rotation is +2.24° and -2.24° respectively. Hence this compound is an example of optical isomerism.
Example: d-, l- and meso-tartaric acid are three compounds. They have molecular formula (C4H6O6), structure formula [HOOC.CH(OH).CH(OH).COOH] and almost all physical and chemical properties but their optical activities are +12°, -12° and 0° respectively. Hence these three compounds are optical isomerism of each other.
Note: – It is possible to sort one or more pairs of optical isomerism whose specific rotation is similar in magnitude but opposite in direction.
The prefixes d-, l- and meso- preceded by the names of optical isomerism show that those isomers are dextrorotatory, laevorotatory and optically inactive, respectively.
The homologous mixture of d- and l- lactic acid is called dl-lactic acid or racemic mixture of d- and l- lactic acid. Similarly, a homogeneous mixture of d- and l- and l-tartaric acid is called the racemic mixture of dl-tartaric acid of dl-tartaric acid and l-tartaric acid. The optical activity of the racemic mixture is zero.
Explanation of Optical Isomerism
Wislicenus first highlighted the cause of optical isomerism in 1865.
According to wislicenus, there is a difference in the relative positions of atoms and groups present in the molecules of optical isomerism. By this time, all four combinations of carbon were considered to be in the same plane. In 1874, le bell and vant hoff hypothesized that the four valences of carbon are directed from the center of a regular tetrahedron to its edges, and on this basis explained optical isomerism.
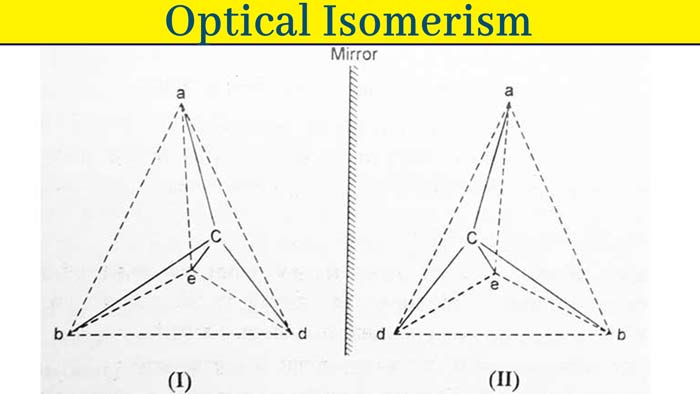
Suppose a compound is Cabde. Four different groups a, b, d and c are attached to one carbon atom in it. Suppose its configuration is i. The mirror image of I will be II. Imagine that by raising II on I, II is fully superimposed on I. It is clear that this is not possible, so I and II are configurations of two different compounds.
This type of compound exhibits optical activity. Its optical activities are equal in magnitude but opposite in direction. These types of compounds are called optical isomerism of each other.
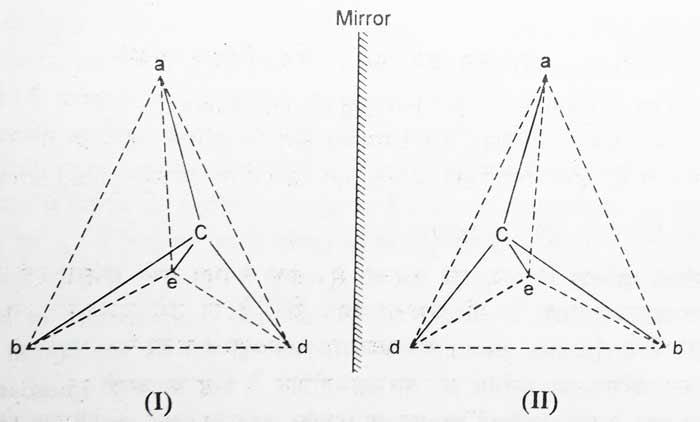
The most suitable method of displaying the configuration of optical isomerism is to make their tetrahedral models, but this method is not convenient. Hence optical isomerism is demonstrated by their fisher projections. Following are the fisher projections of the above configurations I and II.
The groups associated with solid lines displayed in fisher projections are considered to be centered above the floor of the paper and the groups connected with the broken lines. Following is the simple form of fisher projections of both the above configurations –
In simple forms of the above configurations I and II, groups connected by horizontal lines are considered to be centered above the floor of the paper and groups connected by vertical lines are oriented downwards.
Carbon atoms whose four valences are connected to four different atoms and groups of atoms are called asymmetric carbon atom. Hence the carbon atom present in the compound Cabde is asymmetric carbon atom. A compound whose structure contains an asymmetric carbon atom has two possible configurations.
Example: The structure formula of Cabdc additive has two possible configurations I and II. Such compounds exhibit optical isomerism.
-
Importance of Biomolecules in Life || What are the 4 main biomolecules?
-
Valency of Elements || How to Find Valency || What is the Valency of the atom?
-
Resonance effect or mesomeric effect || What is resonance effect with example?
-
Glucose Structure: Physical and chemical properties, Glucose Chemical Reaction
-
Introduction of Inductive-Effect || How does Inductive Effect Work?
-
IUPAC Name : How to find the IUPAC name of compounds.
-
What is Urea || How to make Urea Fertilizer, || Urea uses
-
Sodium Chloride Properties || Why Sodium Chloride is Soluble in Water
If the structure of a compound contains an asymmetric carbon atom, the total number of optical isomerism is 2. Similarly it can be demonstrated that if the number of asymmetric carbon atom in the structure of a compound is n then some number of its optical isomerism is 2n.
Some number of optical isomerism is less than 2n if n is greater than 2 or 2. In this case the number of possible configurations is only 2n, but some configurations are symmetric due to internal compensation of asymmetry, ie their mirror image is not different from them.
Hence the total number of configurations is less than 2n. This type of optical isomerism which is symmetric is called meso isomer.
When asymmetric carbon atoms are present in a compound, it must exhibit optical isomerism.
The asymmetric carbon atom is also called a chiral center or chiral atom.
Optical isomerism of lactic acid
The molecular formula of lactic acid is C3H6O3 and the structure formula CH3.CH(OH).COOH. It is found in two forms –
d-lactic acid: – It is obtained from the extract of meat. Its specific rotation is +2.24°. It is dextrorotatory substance. It is also called d-lactic acid or (+)-lactic acid, this D-(+) lactic acid.
l-lactic acid: – It is obtained from sucrose by fermentation method. It has a specific rotation –2.24°. It is a laevorotatory substance. It is also called l-lactic acid, (-)-lactic acid or L-(-)-lactic acid.
The d and l letter and (+) and (-) sign in the above names represent the direction of optical activity. D and L demonstrate the feature of letter configuration.
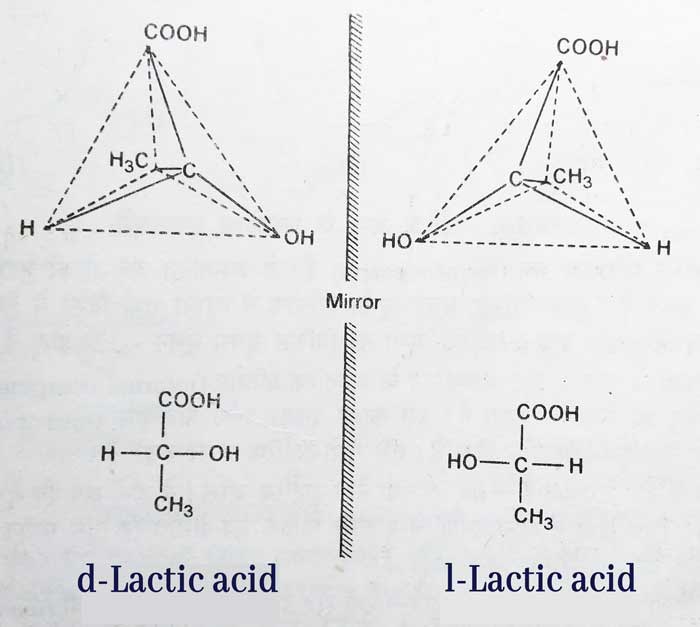
The configuration of d – and l – lactic acid is as above–
An asymmetric carbon atom is present in the structure of these acids. This atom is associated with four different atoms and groups(H, CH3, COOH and OH).
Therefore, according to the 2n rule, only two optical isomerism is possible. These isomerism mirror each other. Hence their optical activities are equal in magnitude and opposite in direction. All other physical and chemical properties of d- and l-lactic acid are the same. Hence, these two are optical isomer of each other.
The equimolecular mixture of d- and l- forms of lactic acid is called dl-lactic acid, racemic lactic acid or d- and l- lactic acids as racemic mixture. This mixture is optical activity due to external compensation of asymmetric. It is obtained from sour milk or from d- or l- form racemisation.
Optical Isomerism of Tartaric Acid
The molecular formula of tartaric acid is C4H6O6. Its structure formula is the following –
HOOC.CH(OH).CH(OH).COOH
Two asymmetric carbon atom are present in the above structure. Therefore, according to the 2n rule, it is possible to have four or less optical isomer. Depending on its structure, it has three optical isomerism possible. Following is the configuration of these isomerism.
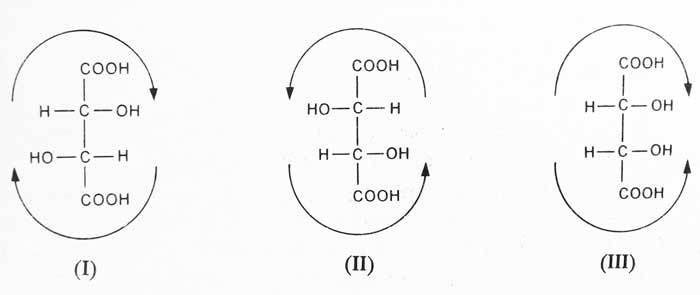
I and II are enantiomer of each other. These represent asymmetric atoms. These are called d- and l- tartaric acid respectively. Their specific rotation is equal in magnitude and opposite in direction. The specific rotation of d- tartaric acid is +12° and the specific rotation of l- tartaric acid is -12°.
As demonstrated by the arrow sign III shows an asymmetry molecule due to internal compensation of asymmetry. Because of this the mirror image is identical to it and it is optical activity. This is called meso tartaric acid.
Therefore, tartaric acid has three forms: – d-, l- and meso tartaric acid. These three forms are optical isomerism of each other. Their optical activities are different but they have the same physical and chemical properties. The equimolecular mixture of d- and l- tartaric acid is called dl- tartaric acid.
Optical isomers that are not mirror images of each other are called diastercoisomers. Hence I and III are diastereoisomers of each other. Similarly II and III are also diastereoisomers of each other.
Optical Isomerism Conditions
A) The tartaric acid molecule has two asymmetric carbon atom. The maximum number of optical isomerism of a compound with two asymmetric carbon atoms is 4 according to the 2n rule.
Since both asymmetric carbon atom present in the molecule of tartaric acid are identical to each other, both carbon atom are connected to the same groups, so two of its four possible configurations are identical to each other and some number of ischemic optical isomerism are 3.
Other similar compounds, which have two similar asymmetric carbon atom, also have 3 optical isomerism.
Example:
CH3 – C*H(OH) – C*H(OH) – CH3 [Butane-2,3-diol]
The above compound has star carbon atoms asymmetric carbon atom and is uniform. Hence the above compound has three optical isomers. One of these d- isomer is second l- isomer and third is meso- isomer.
B) Compounds that have dissimilar asymmetric carbon atom have 4 optical isomerism. No configuration of these compounds can be divided into two equal parts. Their four configurations differ from each other.
Example: Following is the configuration of four optical isomerism of 2,3-dihydroxybutanoic acid.
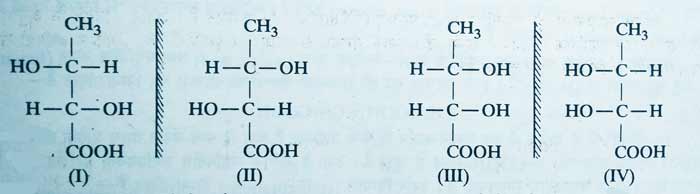
In these, I and II are mirror images of each other. III and IV are mirror image of each other. I and III, I and IV, II and III and II and IV are diastereo isomer of each other.
C) The prefix used in the names of optical isomerism represents the dextrorotatory, laevorotatory direction of optical activity, respectively. The prefixes (+) and (-) also display the dextrorotatory, laevorotatory direction, respectively.
The prefixes D and L do not reflect the direction of optical activity. The prefixes display the attributes of D and L configurations.
The prefixes demonstrate the similarity of the configuration of D and L compound to the configuration of D-glyceraldehyde and L-glyceraldehyde respectively.
