Laws of Osmotic Pressure: Isotonic Solution and Numerical Examples

Laws of Osmotic Pressure

Van’t Hoff studied the effect of concentration and heat on the osmotic pressure of dilute solutions. Van’t hoff pointed out that the concentration and temperature effect on the osmotic pressure of dilute solutions is similar to the effect of these factors on the pressure of gases. On this basis, van’t hoff proposed the following theory which is called theory of dilute solutions.

In dilute solutions, a solute behaves like a gas and the osmotic pressure of the solution is equal to the pressure that the solute will give in a gaseous state while its volume and temperature are equal to the volume and temperature of the solution.

Based on this theory, van’t hoff used gaseous rules for osmotic pressure, the result of which is as follows –

Van’t Hoff-Boyles law

The osmotic pressure of a solution at constant temperature is proportional to its concentration.

If the osmotic pressure of the solution is P, the concentration C of the solution and the volume of the solution in which a certain amount of the solute has dissolved V, then –

P ∞ C

P ∞ 1 / V

PV = constant

van’t Hoff-Charles law

At constant concentrations the osmotic pressure of a solution is proportional to its ultimate temperature. If the osmotic pressure of the solution is P and the ultimate temperature is T, then –

P ∞ T

P/T = Constant

Common Solution Equation: Combining both the above rules

P ∞ CT

P ∞ (n / V) x T

Where n is the number of moles of solute.

P = S x (n/V) x T

PV = nST

This equation is called a normal solution equation. S is a constant. This is called Solution Constant. The value of S is also 0.0821 litre atmosphere per mole per degree ultimate temperature, as in universal gas constant R.

Limitations of the general solution equation: This equation can only be used for solutions of non-volatile materials and for dilute solutions. For substances that dissociate or compute in a solution, ‘i x n’ will be written in place of ‘n’ in the general solution equation, where i is the van’t hoff coefficient and n is the number of moles of the solute.

i = normal number of particles after separation or computation / number of particles

Osmotic pressure and molecular weight

If the w gram of a solute is dissolved in a solution and the molecular weight of the solute is M, then –

Number of moles of solute = n = w/M

According to the general solution equation PV = nST –

PV = (w/M)ST

M = w x S x T/P x V

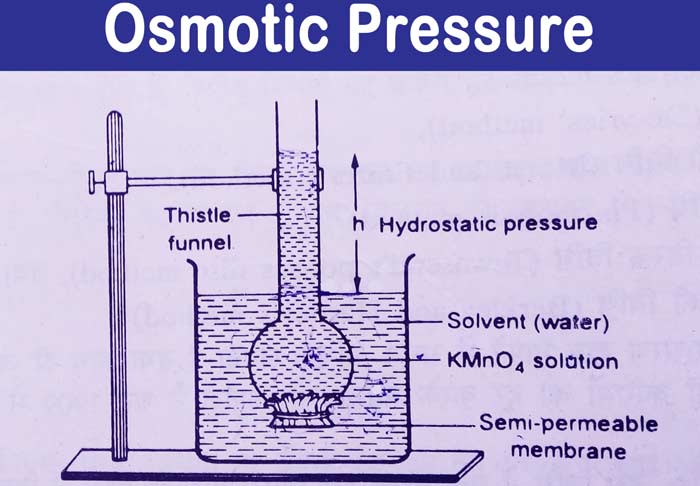
Osmotic-Pressure

Based on the above equation, the molecular weight of a solute can be calculated when the osmotic pressure is known.

Substances that dissociate or compute in a solution. The molecular weights known to them from the above equation are more or less than normal and are called abnormal molecular weight.

Abnormal Molecular weight = i x (w x S x T/P x V)

In order to find the molecular weight of such solutes, i x n will be written in place of n in the general solution equation. on this basis –

M = i x ( w x S x T/P x V)

Normal Molecular Weight = i x ( w x S x T/P x V)

Normal Molecular Weight = i x Abnormal Molecular Weight

Normal Molecular Weight / Abnormal Molecular Weight = i

Normal Molecular Weight/Abnormal Molecular Weight = normal number of particles after separation or computation/number of particles

Isotonic Solution

Solutions that have the same osmotic pressure at the same temperature are called isotonic solution. Due to the osmotic pressure being the same, the osmotic action does not take place when these solutions are separated by a semi permeable membrane, ie the molecules of the solvent do not move from one solution to another. According to the general solution equation PV = nST –

For First Solution: P₁V₁ = n₁ST₁

For Second Solution: P₂V₂ = n₂ST₂

P₁ = P₂

T₁ = T₂

n₁/V₁ = n₂/V₂

Therefore, the molar concentrations of Isotonic solutions are equal.

Hypertonic Solution

In two solutions at the same temperature whose osmotic pressure is higher, it is called hypertonic solution.

Example: Sodium chloride solution acts as a hypertonic solution when the egg is placed in a saturated solution of sodium chloride by removing the outer shell.

Hypotonic Solution

In two solutions at the same temperature whose osmotic pressure is lower, it is called hypotonic solution.

Example: When the egg is placed in a saturated solution of sodium chloride by removing the outer shell, the inner solution acts as a hypotonic solution.

Numerical Examples

Question: Find the osmotic pressure of M/10 solution of urea at 27°C! (R = 0.082 liter atmosphere per degree per mole)

Solution: In Normal solution equation PV = nST

n/V = molar concentration = 1/10 mole per litre

S = R = 0.082 liter-atmosphere/degree/mole

T = 273 + 27 = 300°A

P = (n/V)ST

= 1/10 x 0.082 x 300

= 2.46 atmosphere

Question: Calculate the osmotic pressure of 5% urea solution at 0°C!

(C = 12, O = 16, N = 14, H = 1 and S = 0.0821 litre atmosphere/degree/mole)

Solution: The quantity of urea is 5 grams in 100 ml of 5% urea solution. So the quantity of urea in 1 litre solution will be 50 gram. The molecular weight of urea (NH₂CONH₂) is 2 x 14 + 4 x 1 + 12 + 16 = 60. Hence the number of moles of urea will be = n = 50/60 = 5/6.

V = 1litre

S = 0.0821 litre-atmosphere/degree/mole

T = 0 + 273 = 273°A

P = (n/V)ST

= 5/6 x 0.0821 x 273

= 18.67 atmosphere

Question: 100 grams of a substance is dissolved in 4.5 grams of the substance. The osmotic pressure of this solution at 20°C is 3.2 atmosphere. Calculate the value of R if the molecular weight of the substance is 342.

Solution: In normal solution equation PV = nST-

n = weight in gram/molecule weight = 4.5/342

V = 100/1000 = 0.1 litre

S = R

P = 3.2 atmosphere

T = 273 + 20 = 293°A

Therefore 3.2 x 0.1 = 4.5/342 x R x 293

R = 0.083 litre-atmosphere per degree per mole

Question: The osmotic pressure is 0.025 atmosphere at 27°C of a substance with a concentration of 5 Gram per litre. Find the molecular weight of the substance.

Solution: Let M be the molecular weight of the substance. Hence the number of moles of the substance –

n = 5/M

In normal solution equation PV = nST –

P = 0.025 atmosphere

S = 0.0821 litre-atmosphere per degree per mole

V = .1 litre

T = 273 + 27 = 300°A

Therefore 0.025 x 1 = 5/M x 0.0821 x 300

M = 4926

Question: What will be the osmotic pressure of a 0.05N solution of sucrose at 6°C? Find the concentration of that solution of glucose. Which would be isotonic of this solution of sucrose.(Molecule weight of sucrose = 342, Molecule weight of glucose = 180, S = 0.0821 litre-atmosphere)

Solution: Assuming the molecular weight of sucrose is equal to its equivalent weight. Hence the molar concentration of sucrose solution will be 5M. According to normal solution equation osmotic pressure of sucrose PV = nST –

P = (n/V)ST

= 0.05 x 0.0821 x (273 + 6)

= 1.145 atmosphere

The molar concentrations of isotonic solutions are equal. Therefore, the molar concentration of glucose will also be 0.05M.

Question: A solution of 8.6 gram per litre urea (molecule weight = 60) was isotonic to a 5% solution of an evaporative organic material X. Calculate the molecular weight of X.

Solution: The values of P, S and T are the same in the equation PV = nST for isotonic solutions. Hence their values of n/V are also same.

Molar concentration of urea = concentration in gram per litre/molecule weight

= 8.6/60

There is 5 gram X dissolved in 100 ml of 5% solution of X. So the amount of X in its 1 litre will be 50 gram. Hence concentration in its gram per litre is 50 gram per litre and

Molar concentration of X = molecular weight of 50/molecular weight of X

8.6/60 = 50 / Molecular weight of X

Molecular weight of X = 50 x 60/8.6 = 348.8