Definition of the Rate Constant and Equilibrium Constant

Reaction Rate Constant

Let the equation of a reaction be as follows.

A + B = Products

According to law of mass action:

Reaction Rate ∞ [A] x [B]

Reaction Rate = k [A] x [B]

Here k is a constant called the rate constant of this reaction.

If [A] = 1 and [B] = 1 then the velocity of reaction = k

Hence, the rate constant of a reaction is equal to the velocity of the reaction when the reactants are unit molecular concentrations. Therefore, the Rate constant is also called the specific reaction rate.

The value of the rate constant depends on the nature and heat of the reaction. At constant temperature, the value of the rate constant of a reaction is constant and fixed. The value of the rate constant does not depend on the concentrations or pressures of the reactants.

Effect of heat on Rate constant: The effect of heat on rate constant is represented by the Arrhenius equation. The following is the Arrhenius equation.

Here k is the rate constant, A is the frequency factor, E_a is the energy of activation, R is the universal gas constant and T is the ultimate temperature. A and E_a are characteristics of the reaction. The values of A and E_a are always the same for any one reaction. The values of A and E_a are different for different reactions.

If T₁ and T₂ are rate constant k₁ and k₂ of a reaction on heat then according to Arrhenius equation:

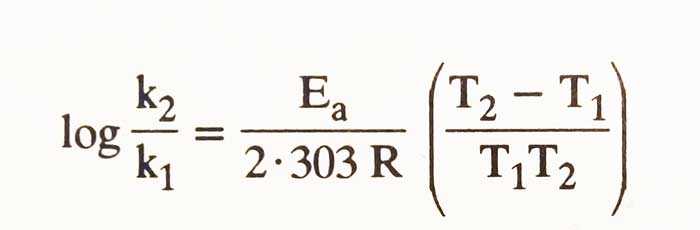
It is clear that the rate constant of each reaction also increases with increasing temperature. Accordingly, the velocity of the reaction also increases. It has been found that at 10°C temperatures the velocity of most reactions doubles.

Effect of catalyst on rate constants: In the presence of positive catalyst, the value of energy of activation (E_a) decreases, so the value of rate constant increases.

Equilibrium constant

Let the equation of a reversible reaction be as follows.

A + B ⇋ C + D

According to law of mass action:

Reaction Rate ∞ [A] x [B]

Reaction Rate = k₁ [A] x [B]

Where k₁ is the rate constant of the forward reaction.

Like this

Reaction Rate ∞ [C] x [D]

Reaction Rate = k2 [C] x [D]

Where k₂ is the rate constant of the backword reaction.

Once the chemical equilibrium has taken place –

Forward Reaction Rate = backward reaction Rate

k₁ [A] x [B] = k2 [C] x [D]

k₁ / k₂ = [C] x [D] / [A] x [B]

K_c = [C] x [D] / [A] x [B]

K_c is called equilibrium constant. The equilibrium constant of a reversible reaction is equal to the ratio of Rate constants of the forward reaction and the backward reaction.

Molar concentrations of the products in the expression of K_c are written in the numerator and molar concentrations of the reactants in the denominator. The subscript c of K_c shows that molar concentrations are used to the reactants and products in the expression of K_c.

The expression of equilibrium constant represents the concentration at the equilibrium of the reactants and products. Any time the product of concentrates of products is divided by the product of the concentrations of the reactants, the quotient is called reaction quotient and it is represented by Q.

• Electric Potential Energy : Electric Dipole, Potential Gradient
  
• Coulomb's Law : Electric Field, Potential Difference, Volt
  
• Gauss Law or Gauss Theorem : Solid Angle and Electric Flux
  
• Electrolysis : Definition, Principle and Electrolytic Cell
  
• Adsorption : Adsorption rate, Physisorption and Chemisorption
  
• Electric Cell : E.M.F., Terminal Potential, Internal Resistance
  

For the following general reaction –

aA + bB ⇋ cC + dD

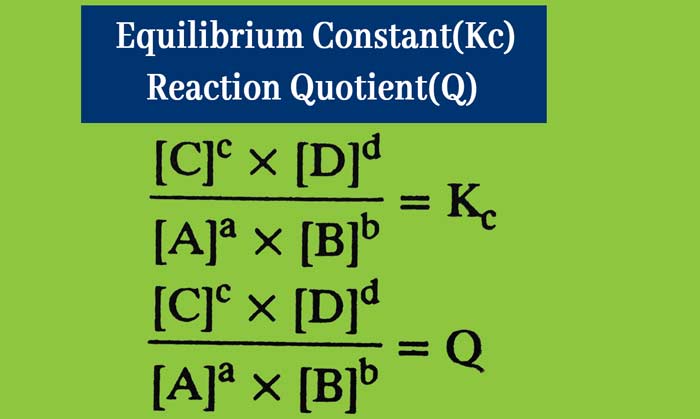
If Q < Kc then the reaction takes place in the forward direction.

If Q > Kc then the reaction takes place in the backward direction.

If Q = Kc then the reaction occurs in equilibrium.

Difference between rate constant and equilibrium constant

If the rate constant of the forward reaction of a reversible reaction is K₁, the rate constant of the backward reaction K₂ and the equilibrium constant K_c, then-

K_c = K₁ / K₂

Like the rate constant, the value of equilibrium constant also depends on the nature and heat of the reaction. At constant temperature, the value of the equilibrium constant of a reversible reaction is constant and fixed. Like the rate constant, the value of equilibrium constant also does not depend on the concentrations or pressures of the reactants and products.

The presence of a catalyst changes the value of the rate constant. The presence of a catalyst has the same effect on forward and backward reactions and does not change the value of equilibrium constants.

Equilibrium constants of Forward and Backward reactions

For the following reversible reactions –

A + B ⇋ C + D

Equilibrium constant of forward reaction (K_c) = [C][D]/[A][B]

Equilibrium constant of opposite reaction (K_c’) = [A][B]/[C][D]

Therefore K_c = 1/K_c^’

Hence, the equilibrium constants of the forward and backward reactions of a reversible reaction are inverse to each other.

Equilibrium constants of Forward and Backward reactions

Equilibrium constant of forward reaction (K_c) = [C][D]/[A][B]

Equilibrium constant of opposite reaction (K_c’) = [A][B]/[C][D]

Therefore K_c = 1/K_c^’

Hence, the equilibrium constants of the forward and backward reactions of a reversible reaction are inverse to each other.

The equilibrium constants of chemical reactions depend on their equations. If the equation of a chemical reaction is written in a different form, the value of its equilibrium constant will change.

Example: The equation of thermal dissociation of nitrogen dioxide can be written as:

2NO₂ ⇋ N₂ + 2O₂

For the above reaction –

Equilibrium constant (K_c) = [N₂][O₂]² / [NO₂]²

The equation of thermal dissociation of hydrogen dioxide can also be written as-

NO₂ ⇋ ½ N₂ + O₂

For the above reaction-

Equilibrium constant (K_c’) = [N₂]^1/2[O₂]/[NO₂]

According to equations 1 and 2 –

K_c = (K_c’)²

It is clear that according to both the above equations different values of equilibrium constants are obtained, that is, the value of equilibrium constant depends on the equation of reaction.

Therefore, to write the value of equilibrium constant one should use the standard equation of reaction or the given equation, the equation should not be changed by multiplying or dividing the number of molecules represented in the equation.

Equilibrium constants of gaseous reactions

According to the ideal gas equation –

PV = nRT

P = n/V x RT

P = CRT

Where C = n / V = number of moles / volume in liters = molar concentration

The partial pressure of a gas is proportional to its molar concentration by constant heating according to the above equation.

For this reason, partial expressions of gases can be used instead of molar concentrations in the expression of equilibrium constants of gaseous reactions. In this case, the equilibrium constant is represented by K_p.

Let the equation of a reversible gaseous reaction be as follows –

A(g) + B(g) ⇋ C(g) + D(g)

Using the law of mass action on this reaction, the values for the reaction constants K_c and K_p will be as follows –

K_c = [C] x [D] / [A] x [B]

K_p = P_C x P_D / P_A x P_B

P_A, P_B, P_C, and P_D are partial pressures of A, B, C, and D at equilibrium, respectively.

Relationship between Kp and Kc

Let the equation of a reversible gaseous reaction be
as follows:

aA(g) + bB(g) ⇋ cC(g) + dD(g)

In the above reaction, A and B are reactants and C and D are products. a, b, c and d are the numbers of their molecules.

All reactants and products are in gaseous state. Using the law of mass action on this reaction, the values of K_c and K_p will be as follows –

K_c = [C]^c x [D]^d / [A]^a x [B]^b

K_p = P_C^c x P_D^d / P_A^a x P_B^b

According to the ideal gas equation-

PV = nRT

P = n/V x RT

P = CRT            where C is molarity

P_A = C_ART = [A] x RT

P_B = C_BRT = [B] x RT

P_C = C_CRT = [C] x RT

P_C = C_DRT = [D] x RT

Put the value of P_A, P_B, P_C and P_D in the equation

K_p = [C]^c (RT)^c [D]^d (RT)^d / [A]^a (RT)^a [B]^b (RT)^b

K_p = [C]^c x [D]^d / [A]^a x [B]^b x (RT)^c+d-a-b

K_p = K_c x (RT)^Δn

Where Δn there is a difference of the number of molecules of the products and the reactants.

Units of equilibrium constant

The expression of equilibrium constant K_c contains the terms of molar concentrations. Molar concentrations are expressed in mole per liter.

Hence the unit of K_c is (mol/liter)^Δn.

Where Δn = number of molecules of products – number of molecules of reactants

Similarly, the expression of equilibrium constant K_p includes pressure terms. The pressure is expressed in the atmosphere, so the unit of K_p is (atmosphere)^Δn, where Δn is the difference between the number of molecules of the products and the reactants.

It is clear that the unit of K_c and K_p depends on the type of reaction.

If Δn = 0 i.e. the number of molecules of the products is equal to the number of molecules of the reactants then K_p = K_c and K_p and K_c have no units.

The value of R is 0.0821 liter-atmosphere mole^-1 K^-1. The value of T is usually around 300 K so the value of RT is greater than 1.

Therefore, if Δn is positive, that is, the number of molecules of the products is greater than the number of molecules of the reactants, then K_p > K_c. If Δn is negative, that is, the number of molecules of the reactants is greater than the number of molecules of the products, then K_p < K_c.

Following are examples of reactions in which the number of molecules changes.

1)   N₂(g) + 3H₂(g) ⇋ 2NH₃(g)

K_c = [NH₃]² / [N₂][H₂]³

Unit of K_c = (mol per liter)^-2

= liter^-2 mol^-2

K_p = PNH₃² / PN₂ x PH₂³

Unit of K_p = (atmosphere)^-2

2)   2NO₂(g)  ⇋ N₂(g)  + 2O₂(g)

   Kc = [N₂][O₂]² / [NO₂]³

Unit of K_c = (mol per liter)¹

        = mol per liter

    K_p = PN₂ x PO₂² / PNO₂²

Unit of K_p = (atmosphere)¹

Effect of heat on equilibrium constant

Equilibrium constant K_c = rate constant of forward reaction(k₁) / rate constant of opposite reaction(k₂)

The value of rate constant increases with increasing temperature.

Therefore, the values of k₁ and k₂ increase with increasing temperature. If the value of k₁ increases in greater proportion then the value of K_c will increase. If the value of k₂ increases in greater proportion then the value of K_c will decrease.

Therefore, the value of rate constant always increases with increasing temperature but the value of equilibrium constant can also increase and decrease.

Van’t Hoff studied the effect of heat on equilibrium constants based on the principles of thermodynamics and established the following relations –

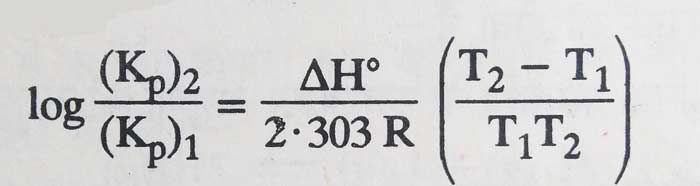
Where T1 and T2 are equilibrium constants (Kp)1 and (Kp)2 at absolute temperature, R is the universal gas constant and ΔH is  reaction heat of forward-reaction in the constant pressure.

Where T1 and T2 are equilibrium constants (Kc)1 and (Kc)2 at absolute temperature, R is the universal gas constant and ΔE° is the reaction heat of the forward reaction at constant volume. For liquid systems, one can also write ΔH° in place of ΔE° in the above equation.

Both the above relations can also be obtained with the help of arrhenius equation. In fact arrhenius equation is an empirical equation.

Heat is absorbed in endothermic reactions and the value of ΔH° is positive for these. It is clear that the value of equilibrium constant increases with increasing temperature of endothermic reactions.

Exothermic reactions emit heat and for these the value of ΔH° is negative. It is clear that the value of equilibrium constant decreases with increasing temperature of exothermic reactions.

Importance of equilibrium constant

Calculation of equilibrium concentrations: If the initial concentrations of the reactants are known, the remaining quantities of the reactants and the quantities of the products can be calculated with the help of equilibrium constants.

Measuring the extent of the reaction: With the help of the value of equilibrium constant, it can be told to what extent the authorities have converted into products before the equilibrium was established.

example:

The value of the equilibrium constant of the reaction at 1000 K is 2.2×10²².

2CO(g) + O₂(g) ⇋ 2CO₂(g)

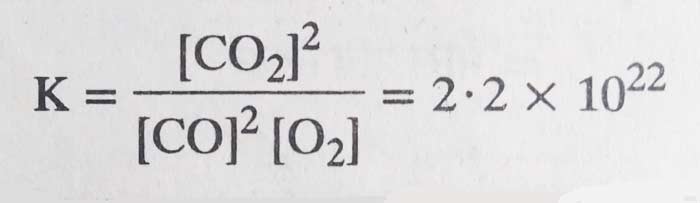
It is clear that the concentration of CO₂ at equilibrium is much higher than the concentrations of CO and O₂, that is, the reactants have been converted into almost complete product. Therefore, the higher the value of K, the greater the tendency for the reaction to be in the forward direction.

Stability of products: With the help of the value of equilibrium constant, the relative stability of the reactants and products is obtained. If the value of K is high then the products are more permanent and if the value of K is less then the products are less permanent.

Example:

N2 + O₂ ⇋ 2NO                              K = 5 x 10^-31

N2 + 2O₂ ⇋ 2NO₂                          K = 2 x 10^-31

Comparing the equilibrium constants of these
reactions, it is found that NO is more stable than NO₂.