Binding Energy of the Nucleus Nuclear Stability and Mass Defect
Nuclear Stability
There are three types of fundamental particles in an atom, electron, proton and neutron. Of these, protons and neutrons are in the nucleus of the atom and electrons are outside the nucleus of the atom.
The volume of the atom’s nucleus is much less than the volume of the atom. Since protons are positively charged. And similar charges repel each other, so due to repulsion of protons, all nuclei should be temporary.
In addition to the radioactive atom, the nuclei of all other types of atoms are permanent. So far 112 elements have been discovered. Isotopes of all elements are known. Thus about 2000 nuclei are known. Of these, 279 nuclei are permanent. All other nuclei are temporary.
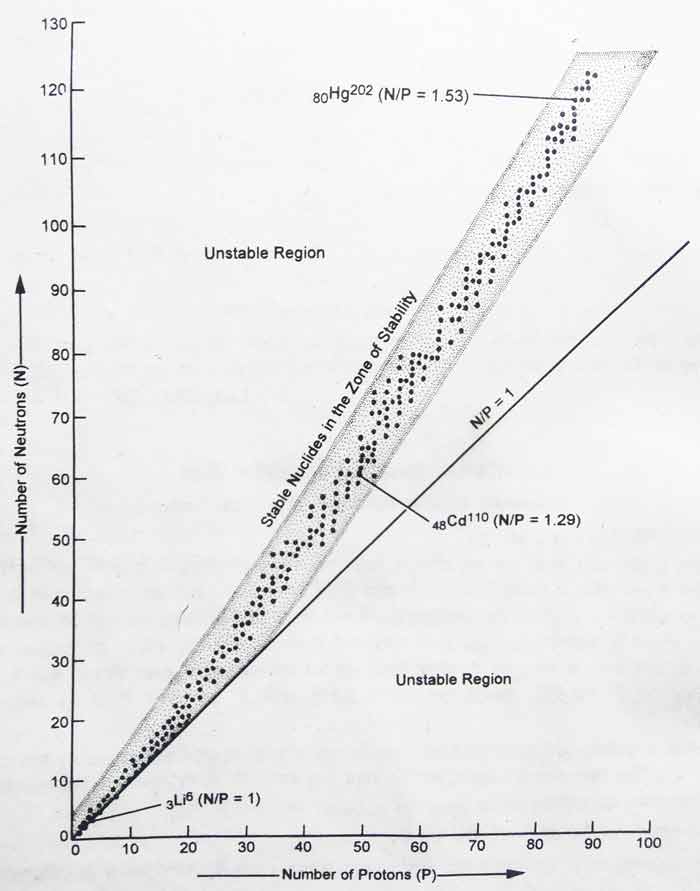
A curve is obtained when the graph is drawn between the number of neutrons and protons present in the nucleus. Each point displayed in the graph represents a permanent nucleus. The shaded area displayed in the graph is called the zone of stability.
1) The value of N/P is about 1 for the stability of light nuclei.
Example: For the nucleus of 3Li6, the value of N/P is 1 and it is permanent.
2) For stability of medium mass nuclei, the value of N/P is between 1 and 1.5. For the 48Cd110, the value of N/P is 62/48 = 1.29 and is constant.
3) For stability of heavy nuclei. The value of N/P is about 1.5.
Example: For 80Hg202 the value of N/P is 122/82 = 1.3 and it is permanent. For 82pb206 the value of N/P is 124/82 = 1.51 and it is permanent.
4) All atoms with 84 or more than 84 atomic numbers have temporary nuclei.
Based on the even and odd numbers of protons and neutrons in the permanent nucleus, the following conclusions are obtained –
| Number of Protons | Number of neutrons | Nuclear Stability | Example |
|---|---|---|---|
| Even | Even | 168 | ₆C¹² , ₈O¹⁶ |
| Even | Odd | 57 | ₆C¹³ , ₂₂Ti⁴⁷ |
| Odd | Even | 50 | ₉F¹⁹ , ₁₁Na²³ |
| Odd | Odd | 4 | ₁H² , ₃Li⁶ |
Mass Defect
The actual masses of atoms are often less than the total mass of their electron protons and neutrons.
Example: The actual mass of an atom of oxygen-16 is 15.9949 amu, while the total weight of 8 electrons, 8 protons and 8 neutrons present in one of its atoms is 8 x 0 .00055 + 8 x 1 .00867 + 8 x 1.00728 = 16 .132 amu. Since the mass of an electron is negligible to the total mass of an atom.
Sum of the electrons, protons and neutrons of the atom – the actual mass of the atom = the sum of the masses of the particles of the nucleus – the actual mass of the nucleus
Hence, the actual mass of nuclei of atoms is often less than the sum of the mass of their protons and neutrons.
This decrease of the mass of the nucleus is called Mass Defect. Mass loss is the sum of the mass of particles present in the nucleus of an atom and the difference between the actual mass of the nucleus.
The mass defect per Nucleon is called packing fraction.
Binding Energy of the Nucleus
The energy that is generated to undermine the repulsive forces of protons in the nucleus of an atom is called the binding energy of the nucleus.
The binding energy of the nucleus is related to the mass defect of the nucleus.
Relation in mass defect and binding energy of the nucleus – according to Einstein, if the material is destroyed, then energy is produced. According to Einstein, mass (m) and the energy (E) produced from it have the following relationship.
According to scientists, the energy produced by the mass defect of the nucleus of the atoms is used to make the nuclei permanent, which is unaffected by the repulsion of the protons in the nucleus.
Therefore, the energy generated in an atom related to mass loss is called its binding energy. If mass is Δm amu then the binding energy
E = (Δm amu) x (3 x 1010 cm/sec)2
= [(Δm gram)/1 gram ] x 1 amu x (3 x 1010 cm/sec)2
because 1 gram = 6.022 x 1023 amu
E = [(Δm gram) /6.022 x 1023 amu ] x 1 amu x (3 x 1010 cm/sec)2
E = Δm x (3 x 1010 )2 / 6.022 x 1023
= Δm x 1.4945 x 10-3
= Δm x 931 MeV
if Δm = 1 then E = 931 MeV
So 1 amu mass defect is equal to 931 MeV binding energy.
1 amu = 931 MeV (millielectronvolt)
If the total binding energy of the atomic nucleus is divided by the number of particles of the nucleus, the binding energy of the nucleus is obtained nucleons per nuclear particle.
Binding energy of nucleus per nucleon = Binding Energy of nucleus / number of nucleons
The binding energy is the measure of the stability of the nucleus of an atom per nuclear particle. The higher the bonding energy of an atom, the more atomic per nuclear particle, and the more stable the atom is.
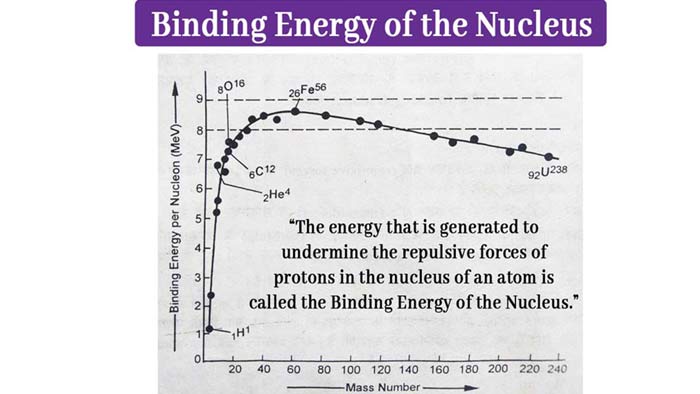
The curve obtained when drawing a graph in the number of binding energy per nucleon and mass is shown in the figure. This curve provides important conclusions regarding the stability of the nucleus.

By observing the curve of binding energy, it is clear that –
i) Atoms whose mass numbers are around 60 – such as iron, cobalt, nickel and copper have the most permanent nuclei. Iron is found in abundance in the earth because the binding energy of 26Fe56 is the highest per Nucleon (Near about 8.7 MeV).
ii) If the light nucleus is combined into a larger nucleus, then in this action the less permanent nucleus will be converted into the more permanent nucleus. This action will emit energy.
Since positively charged nuclei repel each other, it is not easy to initiate the reaction of a nucleus solution, so light nuclei do not attach automatically.
The Sun’s high temperature and hydrogen bomb are the main examples of nuclear fusion.
iii) The points of 4Be8 6C12 and 8O16 are above the normal position in the binding energy curve. Hence the stability of these nuclei is more than normal.
The number of protons and neutrons in them is simple multiplied by the number of protons and neutrons in 2He4.
Hence it can be assumed that their nuclei are made up of 2, 3 and 4 helium nuclei. On this basis, the reason for the emission of a particles from the radioactive substrate can be elucidated.
iv) The binding energy of heavier nuclei such as U-238 is lower than that of nuclei with mean mass numbers per Nucleon, such as Fe-56 Pb-206.
Therefore, in order to achieve stability, the heavy nuclei disintegrate in nature automatically and form permanent nuclei.