What is Friction Force? The angle of Friction | Limiting Friction

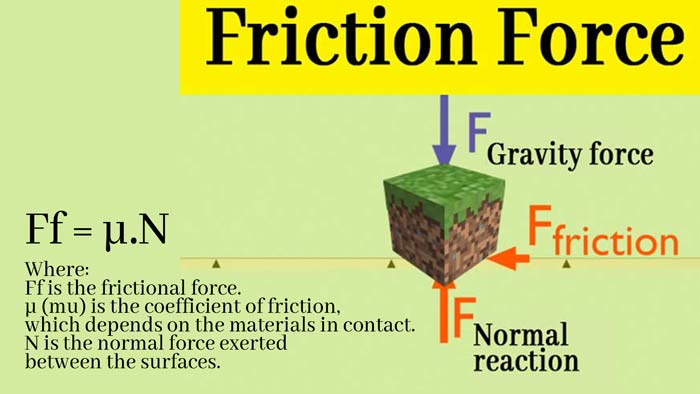
Friction Force

If we push the book on the horizontal table at any speed, then the book comes to rest after running a bit. It is clear from this that there is a force on the book which opposes its motion on the table.

This force is called Friction forces or friction force. And it arises from the interaction between the molecules of the book and the table.

In fact, whenever the surface of one body slips at the bottom of another, each body exerts friction forces on the other body which is parallel to the contact planes of the body. This force is acting on each body in the opposite direction of its relative motion.

Thus, when a book is moved from left to right on the floor of the table, the friction force on the book is on the left side and the same friction force on the table is on the right side.

Friction force between two planes can exist even before relative motion begins.

Suppose a block on the horizontal floor of a table is kept in pause. There are two forces on the block. See Figure (B)

A weight mg which is oriented vertically downward at its gravity center and the reaction force P applied by the table on it is vertical upward and passes through its gravity center.

Since the block is in equilibrium, hence P = mg.

For clarity, the action lines of mg and P have been shown to be somewhat displaced.

Limiting Friction

When we apply a small horizontal force F to the right side on the block, the block does not start moving from its position. See figure (C)

Now, the force F applied to the block by the floor of the table bends to the left so that P, mg, F form a closed triangle. Force P can be divided into two components.

Parallels and verticals of contact planes. The parallel component of the contact planes is called force of static friction (f_s).

And this balances the applied force F. There is a normal reaction R on the block perpendicular to the contact plane which balances the weight mg of the block. (R = mg)

Limiting friction force rules:

Now, even if we give a slightly larger force to the charged force F, the block does not start moving. It is clear from this that the force P bends slightly to the left so that the force of static friction f_s increases again to equal the new force of F.

Thus, as the value of F increases, the Force of Static friction F_s also increases, but f_s may not exceed after a threshold. At this time the block is about to move above the table. This maximum value of force of static friction is called limiting friction force.

• 
  Importance of Biomolecules in Life || What are the 4 main biomolecules?
  
• 
  Valency of Elements || How to Find Valency || What is the Valency of the atom?
  
• 
  Resonance effect or mesomeric effect || What is resonance effect with example?
  
• 
  Introduction of Inductive-Effect || How does Inductive Effect Work?
  
• 
  What is Urea || How to make Urea Fertilizer, || Urea uses
  
• 
  Sodium Chloride Properties || Why Sodium Chloride is Soluble in Water
  
• 
  Glucose Structure: Physical and chemical properties, Glucose Chemical Reaction
  
• 
  Chemicals in Medicine: Class 12
  

Based on several prognostic observations related to friction between different planes, the following rules of marginal friction have been found to be true.

• The magnitude of the marginal force of static friction depends on the nature of the contact planes and their roughness. It does not depend on the size or area of the floors.
• For a given plane, the friction force is tangential to the contact plane and its direction is opposite to the direction in which the block is induced to move.
• The marginal force of static friction f_s for a given plane is directly proportional to the response R.

f_s ∞ R

f_s = μ_sR

Where the sequential constant μ_s is called the coefficient of static friction. The above formula applies only when the value of f_s is maximum as in figure C. Earlier figure B f_s < μ_sR. Hence f_s ≤ μ_sR in general form.

If the force driving the block reverses the direction of F, then the direction of f_s also reverses when there is no change in the direction of R. In fact, the direction of f_s is always opposite to F.

Limiting Friction

Once the motion starts, the friction force applied between the planes decreases and now some less force F is required to maintain uniform motion.

The friction force applied between the planes during motion is called dynamic friction force f_k and its value is less than the marginal coefficient of static friction f_s. We also experience this in our daily life that it requires less force to keep a body moving than resting.

Thus when the block is in uniform motion, the dynamic friction force

f_k = μ_kR

Where μ_k is the coefficient of dynamic friction and its value is less than coefficient of static friction μ_s.

Angle of Friction

In the state of limiting friction, limiting friction force f_s and the resultant P of the response R, the angle it makes with the Normal Reaction R is called the angle of friction. If this angle is θ_s then

tan θ_s = f_s/R

because         f_s/R = μ_s

so that           tan θ_s = μ_s

Thus the coefficient of static friction is equal to the tangent of the angle of friction.

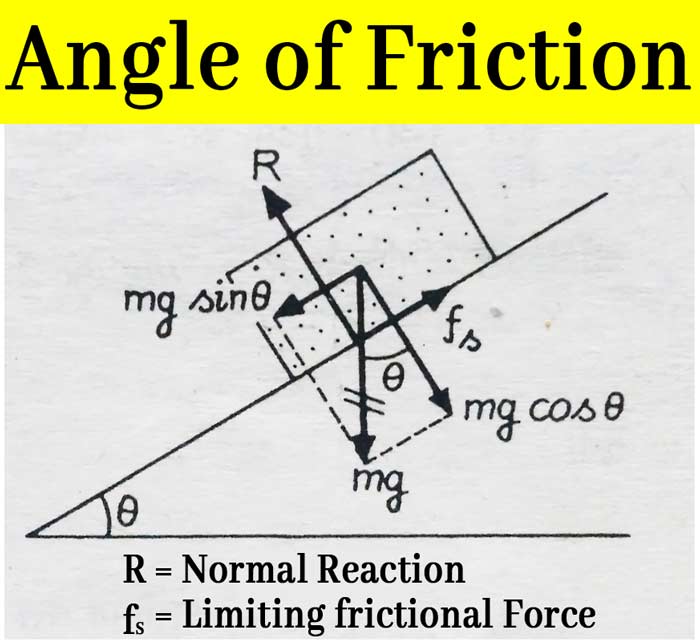
Friction on an inclined plane: In figure a block is placed on such an inclined plane. Which is making θ angle from horizontal. The weight of the block is directed to the mg vertical downward and the vertical response R upward down the floor.

The two components of weight mg, mg sin θ and mg cos θ, are parallel and perpendicular to the floor, respectively. Due to the parallel component mgsinθ, the block has a tendency to slide down on the floor, but the force of static friction f_s imposed on the block by the floor is preventing it from sliding.

Since the block is in equilibrium, the net force on the block is parallel to the floor and perpendicular to the floor.

f_s – mg sin θ = 0

R – mg cos θ = 0

Mg sin θ increases by increasing the tilt angle θ. But at the same time f_s also increases to equal mg sin θ. When f_s rises to the marginal value, the block is about to slip on the inclined plane. Suppose in this case the inclination of the plane is angle θ_s. in this situation

f_s = μ_sR

Putting this value of f_s and θ = θ_s in the above equations

μ_sR = mg sing θ_s

R = mg cos θ_s

So that μ_s = tan θ_s

Therefore, by measuring the angle of repose of the inclined plane at which the block starts sliding, the coefficient of static friction f_s can be found.

Once the block starts sliding, only at an angle of repose θ_k somewhat smaller than θ_s, the momentum on the block’s inclined plane remains the same.

 μ_k = tan θ_k

In this case

Where μ_k is the dynamic friction constant.