Molarity Formula : What is Molarity and Normality with Solved Examples?
Solution
A homogeneous mixture of two or more substances is known as solution.
Each part of a homogeneous mixture has the same composition. Generally the ingredients which are present in a homogeneous mixture in a large amount are called solvent and the ingredients which are in small quantity are called solute.
There are a total of nine types of solutions, depending on which the solid liquid and gas of the solution can be in any state.
Solution of a solid into a solid: example – brass: It is a mixture of zinc (20%) and copper (80%).
Solution of solid in liquid: example- salt solution in water
Solution of solid in gas: example – Smoke: It is the solution of carbon in air.
Solution of liquid in solid: example – jelly
Solution of Liquid in liquid: Example – Alcohol: It is a solution of ethyl alcohol in water.
solution of Liquid in gas: example – water vapor in air
Solution of gas in solid: example – Homogeneous mixture of hydrogen gas and palladium metal
Solution of gas in liquid: example – soda water
Solution of gas into gas: example – air
Solution | Full chapter revision
1. Introduction of solution
2. Classification of solution
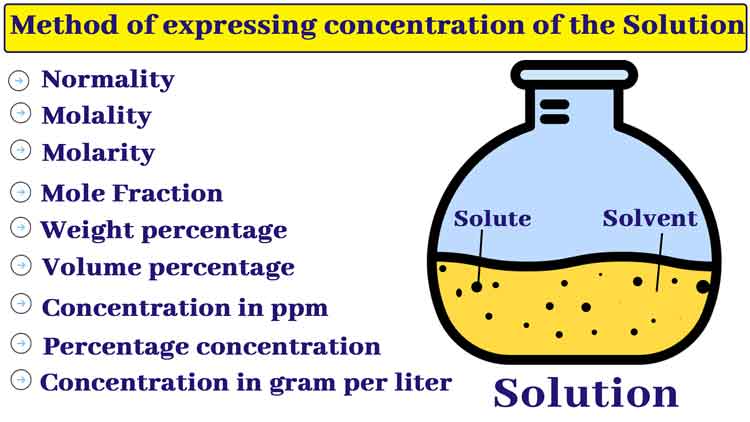
3. Methods of expressing Concentration of Solution
A solution in which the amount of solvent is much greater than that of the solute is called dilute solution. The solution in which the amount of solvent is not much greater than that of the solute is called concentrated solution.
Method of expressing the concentration of the solution
The concentration of a solution represents the ratio of solute and solvent content. The following are the different methods of expressing the concentration of a solution.
Weight percentage of the Solution
The quantity in grams of a solution present in 100 grams of a solution is called its Weight Precentage.

Example: If the concentration of a solution of sodium chloride is 20% (w/w), it means that 20 grams of sodium chloride is dissolved in 100 grams of the solution and the weight of water in the solution is 100 – 20 = 80 grams.
Volume percentage of the solution
The volume in milliliters of a solution present in 100 ml of a solution is called its percentage by volume.

Example: If the concentration of an aqueous solution of ethyl alcohol is 35% (v/v), it means that 30 mL of ethyl alcohol is dissolved in 100 mL of the solution if the change in volume is negligible when ethyl alcohol is added to water. Suppose the water solution will be 100 – 35 = 65 ml.
Percentage concentration
The percentage in grams of solute present in 100 ml of a solution is called its percentage.

Example: If the concentration of a solution is 10%, it means that 10 grams of solute are dissolved in 100 ml of that solution.
- Molarity Formula : What is Molarity and Normality with Solved Examples?
- Glass Material | Composition, Types of Glass, How to make colored glass?
- Ionisation Potential : What are the factors that decide the ionisation potential?
- Fertilizers Chemistry : Types of Fertilizers used in agriculture
- Electric Potential Energy: Definition, Formula and Example | Electrode and Electrode Potential
The parts per million are abbreviated as ppm. The quantity in grams of solute in one million ml (1 million = 106) of a solution is called concentration in its ppm.

Example: If the concentration of a solution of sodium chloride is 106 ppm, it means that 10 ml of sodium chloride is dissolved in 106 ml of the solution.
The concentration of the solution is also displayed in parts per billion, like ppm.
Concentration in gram per liter
The quantity in grams of solute present in 1 liter of a solution is called concentration or strength in its grams per liter.
Example: If the concentration or strength of a solution of NaOH is 40 grams per liter, it means that 40 grams of NaOH is dissolved in a 1 liter solution.

Concentration or strength in gram per liter usually represent as S. If the volume in grams of solute is displayed as w and the volume in ml of solution is shown as V.
 Normality of Solution
Normality of Solution
The number of gram equivalents of a substance dissolved in 1 litre of the solution is known as the Normality of that Solution.
Normality = Number of gram equivalent in the substance / volume in solution in ml
= Weight of substance in grams / Equivalent weight of material X Volume of Liter of Solution
= Weight in grams in 1 liter of substance / Equivalent weight of material
= Strength in grams per liter of substance / Equivalent weight of material
- Molarity Formula : What is Molarity and Normality with Solved Examples?
- Glass Material | Composition, Types of Glass, How to make colored glass?
- Ionisation Potential : What are the factors that decide the ionisation potential?
- Fertilizers Chemistry : Types of Fertilizers used in agriculture
- Electric Potential Energy: Definition, Formula and Example | Electrode and Electrode Potential
Strength (Gram/liter) = Normality X Equivalent
Strength in gram per liter is represent as S, normality as N and Equivalent as E.
S = N x E
w = NEV / 1000
The above formula is very useful for calculating the concentration of a solution.
A solution that has a normality of 1 is called a normal solution. Similarly, the normalities of semi normal and deci normal solutions are 1/2 and 1/10 respectively. These solutions are called N, N/2 and N/10 solutions respectively.
Molarity of Solution
The number of moles of a substance dissolved in 1 litre of the solution is known as the Molarity of that solution.
Molarity = number of moles / volume in litre
= Quantity in grams / molar mass X volume in liter
= Strength in grams per liter / molar mass
Strength (Gram/liter) = Molarity X molar mass
To convert the normality of a solution to molarity and molarity to normality:
Strength (gram/litre) = Normality X Equivalent
= Molarity X Molar mass
Normality X Equivalent = Molarity X Molar mass
Normality / Molarity = Molar Mass / Equivalent
1 mole of an ion has the same amount as its 1 gram-ion mass. Therefore, in order to find the molarity of ions, ion weights will be written in place of experience in the above formula.
Molarity is represented by M. Therefore, M / 10 solution means that the molarity of the solution is 1/10 and M = 1/10.

Molality of solution
The number of moles of a substance that dissolve in a solvent of 1000 grams is called the molality of the solution.
Molality = Number of moles in a solution / Weight of solvent in grams X 1000

Molality is represented by m. If x mole of solute dissolves in W grams of a solvent, the molality of the solution:

Mole Fraction
The ratio of the number of moles of an element present in a solution to the total number of moles present in the solution is called the Mole Fraction of that element in that solution.
If the number of moles of solute in a solution is n and the number of moles of solvent is N, then the total number of moles in the solution will be n + N.
Therefore
Mole fraction of solute = n / n + N
Mole fraction of solvent = N / n + N

The sum of the mole fraction of all the elements of a solution is 1.
Numerical Examples
Question: The tithe of HCl is solubilized in 500 ml of equivalent weight solution. State the normality of the solution?
Answer: Normality of the solution = number of gram equivalents / volume of the solution in liters
= (1/10)/ 0.5
= 1/5
Question: How many grams of this acid will have to be dissolved in 250 ml of water to make 0.1 N solution of oxalic acid
Answer: Equivalent weight of oxalic acid (H2C2O4.2H2O) = weight / n number of equivalents
= (2×1+2×12+4×16+2×18)/ 2
= 126 / 2
= 63
N = 0.1
V = 250
E = 63
W = NEV / 1000
= 0.1 x 63 x 250 / 1000
= 1.575
Question: How many grams of this acid will have to be dissolved in 250 ml of water to make 0.1 N solution of oxalic acid
Answer: Equivalent weight of oxalic acid (H2C2O4.2H2O) = weight / n number of equivalents
= (2×1+2×12+4×16+2×18)/ 2
= 126 / 2
= 63
N = 0.1
V = 250
E = 63
W = NEV / 1000
= 0.1 x 63 x 250 / 1000
= 1.575
Question: Find the normality of the solution made in 1.0 liters of two drops (0.1 ml) 0.1 N H2SO4.
Answer: Number of gram equivalents of H2SO4 = normality x volume in liters
= 0.1 x 0.1 x 10-3
= 1 x 10-5
Normality of dilute solution = number of gram equivalents / volume in liters
= 1 x 10-5 / 1.0
= 1 x 10-5 N