Analog and Digital Circuits : Binary Number System
Analog circuits
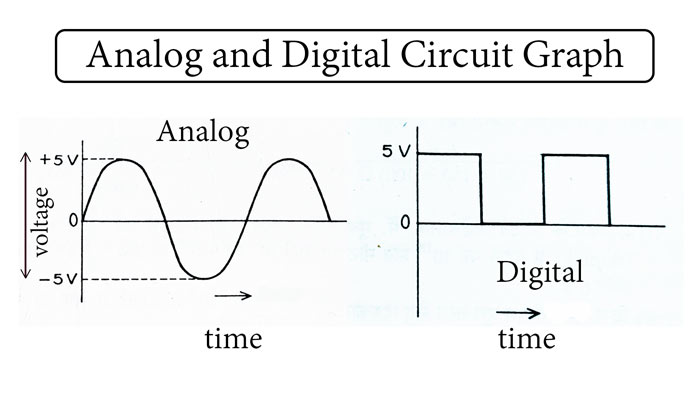
Analog circuits are electrical circuits that use continuous signals to represent information, as opposed to digital circuits which use binary signals to represent information in the form of 0s and 1s. Analog circuits are used in a wide variety of applications, including amplification, filtering, modulation, and demodulation.
One of the main advantages of analog circuits is that they can be designed to perform a wide range of functions, including filtering, amplification, and signal processing. They are also highly adaptable and can be designed to respond to changes in input signals in real-time.

Some common types of analog circuits include operational amplifiers (op-amps), filters, oscillators, comparators, and analog-to-digital converters (ADCs). These circuits can be used in a wide range of applications, including audio systems, medical equipment, communication systems, and instrumentation.
However, analog circuits can be susceptible to noise and distortion, which can negatively impact the quality of the output signal. In addition, the performance of analog circuits can vary based on temperature, humidity, and other environmental conditions, which can make it difficult to design circuits that are reliable and consistent over time.
Digital Circuits
Despite these challenges, analog circuits continue to play a vital role in many areas of electronics and electrical engineering, and they remain an important part of many modern systems and devices.

Digital circuits are electrical circuits that use discrete voltages to represent the two binary values of 0 and 1, also known as “high” and “low”. They are used to design and build digital systems, including computers, communication systems, and control systems.
In digital circuits, signals are transmitted as binary values, which are processed by digital logic gates, such as AND gates, OR gates, NOT gates, NAND gates, and NOR gates. These gates perform logical operations on the binary signals and produce a binary output based on the inputs.
Digital circuits can be designed using various technologies, including field-programmable gate arrays (FPGAs), application-specific integrated circuits (ASICs), and microcontrollers.
In recent years, digital circuits have become increasingly complex and sophisticated, allowing for the development of new and advanced technologies in areas such as artificial intelligence, robotics, and the Internet of Things (IoT).
Number System
A number system is a system for representing numbers in a symbolic form. There are several different number systems in use today, including:
- Importance of Biomolecules in Life || What are the 4 main biomolecules?
- Resonance effect or mesomeric effect || What is resonance effect with example?
- Glucose Structure: Physical and chemical properties, Glucose Chemical Reaction
- Valency of Elements || How to Find Valency || What is the Valency of the atom?
- Introduction of Inductive-Effect || How does Inductive Effect Work?
- IUPAC Name : How to find the IUPAC name of compounds.
Decimal (base-10) system: This is the most common number system used in daily life. It uses 10 digits (0, 1, 2, 3, 4, 5, 6, 7, 8, and 9) to represent numbers.
Binary (base-2) system: This number system uses only two digits (0 and 1) to represent numbers. It is widely used in digital electronics and computer systems.
Octal (base-8) system: This number system uses 8 digits (0, 1, 2, 3, 4, 5, 6, and 7) to represent numbers. It is sometimes used in computer programming.
Hexadecimal (base-16) system: This number system uses 16 digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, and F) to represent numbers. It is commonly used in computer science and digital electronics.
Each number system has its own set of rules for representing numbers and performing arithmetic operations, such as addition, subtraction, multiplication, and division.
Understanding the different number systems and their properties is important for many fields, including computer science, mathematics, and engineering.
Conversion from decimal number system to binary number system:
All calculations outside the computer are done in the decimal number system, while calculations inside the computer are done in the binary number system. Therefore, there is a need to convert the number of decimal system to the number of binary system.
To convert a decimal number into an equivalent binary number, the decimal number is repeatedly divided by 2 until the quotient becomes zero, and the remainder is written in each division. Finally, writing these remainders in reverse order gives an equivalent binary number.

For example, we can convert the decimal number 37 to the equivalent binary number in the following way:
remainder in reverse order 1, 0, 0, 1, 0, 1 .
so 37 is equal to 100101 in binary number.
we can write it as follow :
(37)10 = (100101)2
Same with these numbers :
(21)10 = (10101)2
(43)10 = (101011)2
If the decimal number is a fraction, then to get its equivalent binary fraction, the decimal fraction is repeatedly multiplied by 2, the integer (binary number 0 or 1) obtained in each product is noted separately.
- Importance of Biomolecules in Life || What are the 4 main biomolecules?
- Resonance effect or mesomeric effect || What is resonance effect with example?
- Glucose Structure: Physical and chemical properties, Glucose Chemical Reaction
- Valency of Elements || How to Find Valency || What is the Valency of the atom?
- Introduction of Inductive-Effect || How does Inductive Effect Work?
- IUPAC Name : How to find the IUPAC name of compounds.
And by writing the product numbers 1 or 0 in order from top to bottom, the decimal point is marked at the beginning.
This is the equivalent binary fraction.
For example, we will convert the decimal fraction 0.9375 to the equivalent binary fraction as follows.

Thus, the equivalent binary fraction of the decimal fraction 0.9375 is 0.11110.
(0.9375)10 = (0.11110)2
The point used in a decimal fraction is called a decimal point. Similarly, the point used in binary fraction is called binary point.
If the decimal number has both whole and fraction parts, such as 37.9375, then this decimal number is divided into integer 37 and fraction 0.9375 to get the equivalent binary number.
Then get the binary equivalent of each part separately and combine them. Thus, the binary number equivalent to the decimal number 37.9375 is 100101.11110.
(37.9375)10 = (100101.11110)2