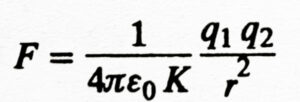
Where K is a dimensionless constant, which is called the dielectric constant or specific inductive capacity of that material and the non-conducting material is called dielectric. The value of K is greater than 1 for all dielectrics.

Therefore, if there is a dielectric between the charges, then the electric force between them decreases.

In the above formula, only e can be written in place of eK and e is called permittivity of that dielectric.

Comparison of electric force with gravitational force

We can compare the electric force acting between two charged objects with the gravitational force acting between them. Both these forces act according to the same laws and both remain active even in vacuum. But there is also some difference between these two:

Electric force can be force of attraction as well as force of repulsion, whereas force of gravity is always force of attraction. This shows that charge can be of two types whereas mass is of only one type.

The electric force depends on the medium between the two charges whereas the gravitational force does not depend on the medium between the two masses.

The electric force is much stronger than the gravitational force. Example: The electric force between two protons is 1036 times greater than the gravitational force between them. Between two electrons it is even greater, that is, 1043 times larger.

Importance of Coulom’s law

The electric force is much stronger than the gravitational force. Example: The electric force between two protons is 1036 times greater than the gravitational force between them. Between two electrons it is even greater, that is, 1043 times larger.

Coulomb’s law is true for very large distances to very small distances, even here for atomic distances (= 10-11 meters) and nuclear distances (= 10-15 meters).

Therefore, this law not only gives knowledge of the forces acting between charged objects, but also helps to explain the forces due to which electrons of an atom bind with its nucleus to form an atom, two or more than one atom binds together to form molecules and many atoms or molecules bind together to form solids and liquids.

The force experienced in our daily life is such a force, which is not the force of gravity, it is an electric force.

Electric field : Electric lines of force

The area around an electric charge or charge community in which some other charge experiences the force of attraction or repulsion is called electric field or electric field force. If a charge placed in an electric field is free to move, then it will start moving in a state of force.

If the direction of force is constantly changing, then the direction of movement of the charge will also change continuously, it will move on a curved path. The path of an independent positive charge in an electric field is called electric line of force.

Electric lines of force is an imaginary, smooth curve drawn in an electric field on which an independent and isolated unit positive charge moves. The tangent drawn at any point to the electric lines of force gives the direction of the force acting on the positive charge at that point. We can represent an electric field by lines of force.

• 
  Importance of Biomolecules in Life || What are the 4 main biomolecules?
  
• 
  Resonance effect or mesomeric effect || What is resonance effect with example?
  
• 
  Valency of Elements || How to Find Valency || What is the Valency of the atom?
  
• 
  Glucose Structure: Physical and chemical properties, Glucose Chemical Reaction
  
• 
  Introduction of Inductive-Effect || How does Inductive Effect Work?
  
• 
  IUPAC Name : How to find the IUPAC name of compounds.
  

Lines of force have been drawn in the electric field generated by a positively charged sphere. If any other positive charge is left free near this sphere, then it will move in a straight line till infinity due to repulsion.

Therefore, the lines of force from a single positive charge go straight to infinity. Conversely, due to a single attraction, it will move from infinity to negative charge. Hence the lines of force running from infinity to a straight negative charge.

For a charged sphere, the lines of force are straight and radial trailing and appear to originate from the center of the sphere or meet at the center.

Lines of force have been drawn in the electric field produced by two equal and opposite charges. These lines run from the positive charge and end at the negative charge.

Lines of force are drawn in the field produced by two equal and equal charges.

For a charged sphere, the lines of force are straight and radial trailing and appear to originate from the center of the sphere or meet at the center.

Lines of force have been drawn in the electric field produced by two equal and opposite charges. These lines run from the positive charge and end at the negative charge.

Lines of force are drawn in the field produced by two equal and equal charges.

At the midpoint N in the line joining these two charges, the field due to one charge is exactly equal but opposite to the field due to the other charge. Hence, the resultant field at this point is Zero. This point is called neutral point. If any other charge is placed at this point then it will not have the tendency to move in any direction.

If both the positive charges are not equal, then the neutral point will not be in the middle. In this case, if the quantities of charges are q1 and q2 and their distances from the neutral point are r1 and r2 respectively, then

q1 / r12 = q2 / r22

Electric field : Electric lines of force

Electric force lines run from positive charge and end at negative charge.

The tangent drawn at any point to the electric force lines shows the direction of the force acting on the positive charge at that point.

No two force lines can intersect, because in that case two tangents can be drawn at the point of intersection which will show two directions of force at that point which is impossible.

These lines try to shrink in length like a stretched string. This is why opposite charges have an attraction.

These lines try to move away from each other in the direction perpendicular to their length. For this reason similar charges have repulsion.

Intensity of Electric Field

To find the value of the field or the intensity of the field at a point in the electric field, a small positive test charge q0 is placed at that point. A force will be applied on this charge.

The force acting on the test charge placed at a point in the electric field and the result of the value of the test charge is called the intensity E of the electric field at that point.

Therefore, if the force F on the test charge q0 placed at a point in the electric field is F, then the intensity of the field at that point is

E = F / q0

force F is a vector quantity and charge q0 is a scalar quantity. Hence, the intensity E of the field will also be a vector quantity and its direction will be the same as the direction of the force F i.e. the direction in which the positive charge placed in the electric field tries to move.

If the test charge is negative rather than positive, then the direction of the electric field E will be opposite to the direction of the force on the (negative) charge.

The unit of force F is Newton and the unit of charge q0 is Coulomb. Hence the unit of electric field E will be newton/Coulomb.

Dimension of Electric field [MLT-3A-1]

Intensity of electric field due to a point charge :

Let the charge of +q coulomb be located at point O in a medium whose dielectric constant is K. In the electric field generated by the charge +q, there is a point P at a distance of r meter from point O at which the intensity of the field is to be determined.

For this, let a positive test charge +q0 be located at point P. According to caulam’s law, the value of the electric force acting on q0

Electric Potential difference and Electric Potential

The electric field produced by a charge can be expressed in two ways.

·      by the intensity of field E at any point in the field

·      by electric potential

E is a vector quantity while V is a scalar quantity and both of them are characteristic properties of any point in the field.

Let +q be a (positive) charge due to which there is an electric field around it. If there is any other positive test charge +q0 in this field, then it will be subjected to an electric repulsive force F due to +q.

So if we move the test charge from point B to point A, we have to do work against the repulsive force.

The work done in moving a test charge from one point to another in the electric field and the resultant value of the test charge is called potential difference between those points.

Therefore, if the work done in moving the test charge q0 from point B to A is W, then the potential difference between A and B is

Work W and charge q0 are both primordial quantities. So the potential difference will also be a scalar quantity.

The unit of work W is joule and the unit of charge q0 is coulam.

The unit of Electric potential difference ( VA – VB ) will be Joule / Coulomb.

It is called Volt.

Therefore, if 1 joule per Coulomb of work is done in moving a test charge from one point to another in an electric field, then the potential difference between those points will be 1 volt.

The potential difference at any point in the electric field is equal to the work done in bringing a test charge from infinity to that point and the conclusion of the value of the test charge.

If 1 joule per Coulomb of work has to be done to bring a test charge from infinity to any point in the electric field, then the potential difference at that point will be 1 volt.

Electron volt or eV: Electron volt is a very small unit of work or energy which is used in physical atom. 1 electron volt is the work that is done to move an electron from one point to another, when there is a 1 volt potential difference between those points.

W = q0 (VA – VB)

If q0 = e = 1.6 x 10-19 Coulomb

1 Electron Volt = 1.6 x 10-19 Joule