Electric Potential Energy : Electric Dipole, Potential Gradient
Two electric charges attract or repel each other. Therefore, some work has to be done in moving the charges away from each other, or in bringing them closer to each other.
This work gets stored in the form of potential energy in the system of those charges. This is called the electric potential energy of the system.

The electric potential energy of a system of charges is equal to the work that is done to make the system by bringing those charges closer to infinity.
Let a system AB be made up of two charges of coulomb +q1 and +q2 which are located at a distance of r meter from each other.
To find the electric potential energy of these systems, assume that the charge +q2 is not at point B but at infinity. Now the electric potential at point B due to charge +q1 :
According to the definition of electric potential, the work done in bringing the charge q2 from infinity to point B is
W = q2V
This work itself is the electric potential energy U of the system (q1 + q2).
If both the charges are of the same type then they repel each other. Then in bringing them closer to each other, work has to be done against the repulsive force, which increases the electric potential energy of the system.
On the contrary, in moving them away from each other, work is done by the system itself, which decreases the potential energy of the system.
If charges are of opposite type, they attract each other. In this case the potential energy of the system decreases when they are brought closer and increases when they are taken away.

Electric potential energy is a scalar quantity. In the formula, the values of charges q1 and q2 are kept with sign. If there are two or more charges in a system, then finding the electric potential energy of each pair of charges and adding them by algebraic method.
Example : If three charges q1 , -q2 , +q3 are at three corners of a triangle, then the electric potential energy of the system
Potential Gradient and Intensity of Electric Field
Let us consider the electric field E along the X-axis due to the +q point charge at point O. Let there be two points A and B respectively at x and x + Δx distances from point O. Let the electric potential at points A and B be V and V – Δv respectively.

Let a small positive test charge q0 be taken from point B to point A in electric field E. A force on charge q0 acts in the direction of the F field
where F = q0 E
Therefore, in moving the charge q0 from point B to A, the external agent will have to do work against the force F. If this work is w then
ΔW = F (-Δx)
where -Δx is the displacement from point B to A.
-E Δx = Δv
E = – Δv / Δx
The amount Δv / Δx is the rate of change of the potential with distance and is called the potential gradient.
- Importance of Biomolecules in Life || What are the 4 main biomolecules?
- Resonance effect or mesomeric effect || What is resonance effect with example?
- Valency of Elements || How to Find Valency || What is the Valency of the atom?
- Glucose Structure: Physical and chemical properties, Glucose Chemical Reaction
- Introduction of Inductive-Effect || How does Inductive Effect Work?
- IUPAC Name : How to find the IUPAC name of compounds.
The intensity of the electric field in a given direction at any point in the electric field is equal to the negative potential gradient in that direction.
The minus sign indicates that the potential decreases in the direction of the electric field.
dimensions of potential gradient = [MLT-3A-1]
Trajectory of a charged particle in a uniform electric field :
The motion of a charged particle in a uniform electric field is the same as that of a projectile in a uniform gravitational field.
Suppose two parallel plates of metal are located at some distance from each other and have opposite charge on them.
The electric field is the same in the space between the plates, except in places near the edges. If the upper plate is positively charged and the lower one is negative-charged, then the electric field E will be directed downwards in the plane of the paper.

Let an electron (-e) moving along the X-axis enter the electric field with a velocity v. The electric field is facing down in the negative direction of the Y-axis. Therefore, there is no force on the electron along the X-axis, but a force F is applied along the Y-axis, whose value is
F = e E
Due to this force, the acceleration produced in the motion of the electron
a = F / m = e E / m
where m is the mass of the electron. force F is directed upwards along the Y-axis. Due to this force the electron gets deflected from its initial path and moves upwards.
Now we will consider the motions of the electron along the X-axis and Y-axis separately. The electron moves along the x-axis with an initial velocity v because there is no significance in this direction. Hence, the distance traveled along the X-axis in t Second
x = vt
The initial velocity of the electron along the Y-axis is zero, but the acceleration of the electron in this direction is a. Hence, the velocity of electron increases in +Y direction. The distance traveled in this direction in t second –
This equation is of the form y = cx2 and represents a parabola. Hence, the path of motion of the electron in the normal electric field is parabolic.
Equipotential Surface
The surface drawn in an electric field on which the potential is equal at all the points is called equipotential surface.
The potential difference between any two points on an equivalent surface is zero. Therefore, no work will have to be done in moving a charge from one point of the equipotential surface to another. But this is possible only when the charge is taken perpendicular to the electric field.
Therefore, the equipotential surface is perpendicular to the direction of the electric field at each point. The force lines at each point of the equipotential surface are perpendicular to the surface.

Force lines running through a point charge +q are drawn. A spherical surface drawn with the point charge as the center will be at the same potential due to being at the same distance from each point charge.
Electric Dipole
Electric Dipole is a system in which two equal, but opposite types of point charges are located at a short distance from each other. The product of the short distance between any one charge and the two charges is called electric dipole moment (p).
Let the charge of Electric Dipole be – q and + q coulomb and the short distance between them is 2l meter. then electric dipole moment
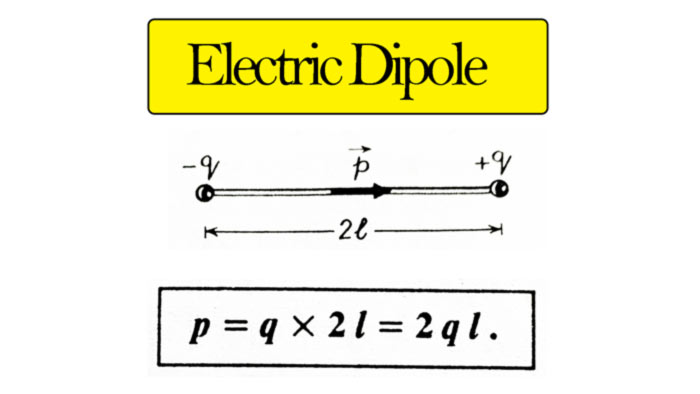
Let the charge of Electric Dipole be – q and + q coulomb and the short distance between them is 2l meter. then electric dipole moment
Electric dipole moment is a scalar quantity whose direction is from negative charge to positive charge along the axis of dipole. Its unit is the coulomb meter (C – m).
Example: There are many molecules like HCl, H2O Electric Dipole.
Moment of Couple on an electric dipole placed in an external uniform electric field :
If we put an electric dipole in an electric field, then a couple of work starts on the dipole. This couple tries to align the dipole in the direction of the field. This is called the restoring couple (τ).
Let an electric dipole be placed in a uniform electric field E making an angle with the field. Let the charges of the dipole be +q and – q and the distance between them is 2l. Due to the electric field E, a force F on the charge +q is in the direction of the field, and on the charge – q, an equal force is exerted in the opposite direction of the field.
If the dipole is placed perpendicular(θ =90° or sinθ = 1) to the electric field
Then the electric dipole moment on it will be maximum.
If it is max then
If E = 1 then p = τmax coulomb-meter
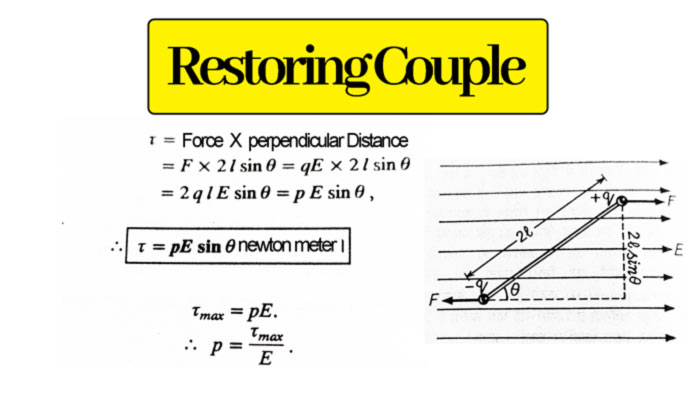
Therefore, an electric dipole moment is that force-couple moment. Which is felt on the dipole when the dipole is kept perpendicular to the direction of a uniform electric field of 1 newton/coulomb.
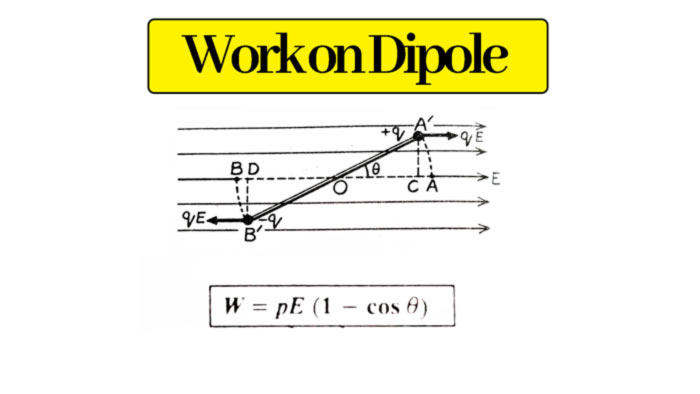
Work done in rotating an electric dipole in an external uniform electric field
In a uniform electric field, work has to be done to rotate the dipole from the equilibrium position.
Let an electric dipole of moment p(= q x 2l) be brought to position A ‘ B ‘ by rotating an θ angle from its time position AP in a uniform electric field E. Due to the electric field E, a force qE on the charge +q of the dipole is in the direction of the field, and an equal force on the charge -q in the opposite direction of the field.
In bringing the charge + q from position A to A’, it is displaced from A to C opposite to the force qE on it. Hence, the work done by the external force on the charge +q
= force on charge (+q) x displacement = qE x AC
Similarly, the work done by the external object in bringing the charge -q from position B to B’ opposite to the force qE on it
= force on charge (-q) x displacement = qE x BD
some work done on the dipole
W = (qE x AC) + (qE x BD) = qE (AC + BD)
But by geometric symmetry, AC = BD
- Importance of Biomolecules in Life || What are the 4 main biomolecules?
- Resonance effect or mesomeric effect || What is resonance effect with example?
- Valency of Elements || How to Find Valency || What is the Valency of the atom?
- Glucose Structure: Physical and chemical properties, Glucose Chemical Reaction
- Introduction of Inductive-Effect || How does Inductive Effect Work?
- IUPAC Name : How to find the IUPAC name of compounds.
W = qE x 2AC
AC = AO – CO
= l – l cosθ
= l (1 – cosθ)
where AO = A’ O = l
W = qE x 2 l (1 – cosθ)
W = qE (1 – Cosθ)
Potential Energy of Electric Dipole in Electric Field: The static energy of an electric dipole in an electric field is equal to the work that is done to bring the dipole within the direction of the field from infinity.
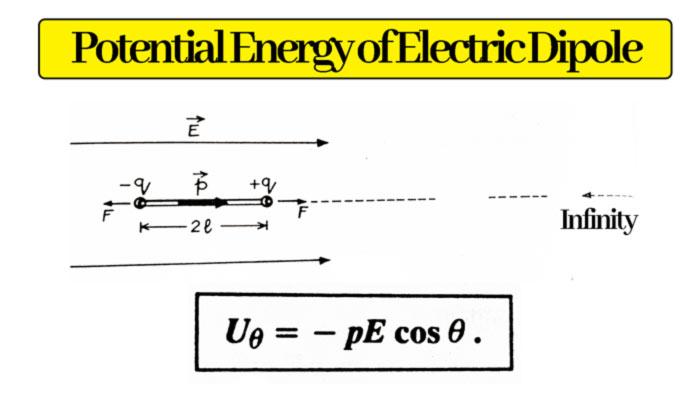
An electric dipole is brought from infinity to a uniform electric field E in such a way that the dipole moment p is always in the direction of the field E. Due to the field E, a force F (=qE) on charge +q of the dipole is in the direction of the field and an equal force F (=qE) on charge -q in the opposite direction. Therefore, to bring the dipole into the field, work will be done by the external agent on charge +q while the field itself will do work on charge -q.
But in coming within the field from infinity, the charge -q has to travel 2l more than the charge +q. Due to this the work done by the field on charge -q will be more and this work will be negative.
So the net work done by the field in bringing the dipole from infinity to infinity is:
= – (force on charge -q ) x extra distance traveled
= – (pE) x 2l = -pE
p – electric dipole moment
This work is the static energy (U0) of the electric dipole located parallel to the field in the electric field :-
U0 = – pE
In this state is in stable equilibrium within the electric field.
Now if we rotate the dipole inside the sphere by angle, then work (W) has to be done on the dipole, where W = pE (1 – cos )
Due to this the static energy of the dipole will increase. Hence, the static energy of the dipole in the position
Uθ = U0 + W = – pE + pE (1 – cosθ )
Uθ = – pE cosθ
This is the equation for the static energy of the electric dipole.
