Gauss Law or Gauss Theorem : Solid Angle and Electric Flux
Gauss Law :
The electric flux ΦE passing through a bonded surface is 1 / Ɛ0 times the total charge q enclosed by that surface.
Before we discuss about gauss law, we must be clear few physical terms here like solid angle and electric flux.
Vector Area
A plane area such as A, has magnitude as well as direction. The direction of the area is the direction of the normal drawn outwards on the area. Thus, area A can be represented by a vector A along the normal drawn outward on it, whose length represents the magnitude A of the area. thus
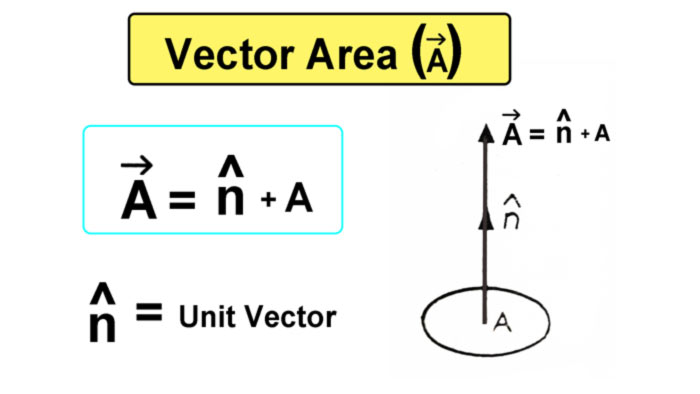
where n̂ is the unit vector along the normal drawn outwards. Vector A is called area Vector.
Solid Angle
We know that the arc, of a circle subtends an angle at the center of the circle. This is called the plane angle. Its unit is Radian (rad). 1 radian is an angle that subtends an arc of length equal to the radius of a circle at the center of that circle.
Gauss Law or Gauss Theorem : Solid Angle and Electric Flux
Electrolysis : Definition, Principle and Electrolytic Cell
Adsorption : Adsorption rate, Physisorption and Chemisorption
Electric Cell : E.M.F., Terminal Potential, Internal Resistance
How Transistor Works : PNP and NPN Transistors
How p-n Junction Diode works : Forward and Reverse Biasing
Similarly, the angle subtended by the area of a spherical surface at the center of the sphere is called a solid angle. And it is denoted by Ω.

Solid Angle Unit
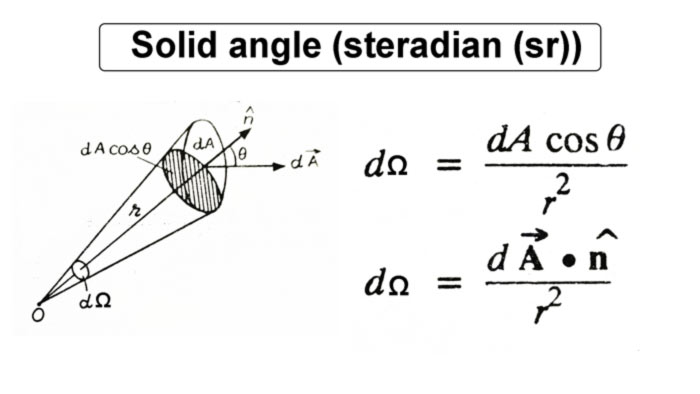
Let the center of a sphere be O and the radius be r. We consider an area element dA on its surface. If the points on the boundary of this area element are joined with the center O of the sphere, then the lines so drawn subtend a solid angle dΩ at the center O.
Since the spherical area dA is directly proportional to the square of the radius r2, the conclusion dA/r2 is a constant. This result is called the subtend solid angle dΩ by the area dA at the center O of the sphere.

The unit of solid angle is called steradian (sr).
if dA = r2 then dΩ = 1
Therefore, the 1 steradian is the solid angle subtended at the center of the sphere by a part of the surface of the sphere whose area is equal to the square of the radius of the sphere.
The area on the entire surface of the sphere is A (= 4pir2). Hence the solid angle subtend at the center of the sphere by the entire surface :

Now , let an area element dA be at a distance r from a point O. Let n be the unit ventor along the line joining point O to the area element dA. Let the angle between n and the vector dA be .
If a sphere of radius r is drawn with point O as center, then the projection of the area element dA on the surface of the sphere will be dAcosθ. Hence, the solid angle subtended by the area element dA at the center O of the sphere.
Electric Flux
Electric flux is a property of an electric area. An electric field can be represented by electric lines of force. Where the electric lines of force are close together, the electric field is strong and where the lines of force are far away, the electric field is weak.
The electric flux on an imaginary surface located in an electric field is a measure of the number of lines of force passing through that surface. It is denoted by ΦE.
The non-uniform electric field is represented by electric lines of force. Suppose an imaginary arbitrary surface is located in this region and dA is a surface element. The surface element dA is so small that it can be considered flat and the electric field on it can be considered ‘similar’.

The surface element dA can be represented by an area vector dA whose magnitude is the area dA of the surface element and whose direction is along the outward normal on the surface element.
Let the electric area be E at the position of the surface element dA. Then the scalar product E.dA is called the electric flux passing through the element.
Electric flux passing through the entire surface:
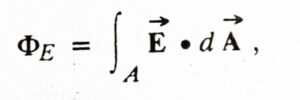
where fA is the surface integral for the whole surface. If the lines of force are exiting the surface, then ΦE is positive, if the lines of force are entering the surface, then ΦE is negative.
Thus, the electric flux associated with a surface in an electric area is equal to the surface integral of the electric area on that surface.
- Importance of Biomolecules in Life || What are the 4 main biomolecules?
- Resonance effect or mesomeric effect || What is resonance effect with example?
- Valency of Elements || How to Find Valency || What is the Valency of the atom?
- Glucose Structure: Physical and chemical properties, Glucose Chemical Reaction
- Introduction of Inductive-Effect || How does Inductive Effect Work?
- IUPAC Name : How to find the IUPAC name of compounds.
If the surface located in an electric area is a closed surface, that is, it is enclosing a volume, then the net electric flux passing through this surface is:
Now, let a plane surface of area A be placed in a similar electric area E in such a way that the normal drawn to the surface makes an angle θ with area E. By definition, the electric flux passing through this surface is:
where dA is the area vector representing the surface element dA. Since the vector dA is normal to the surface, the angle θ between the vector E.
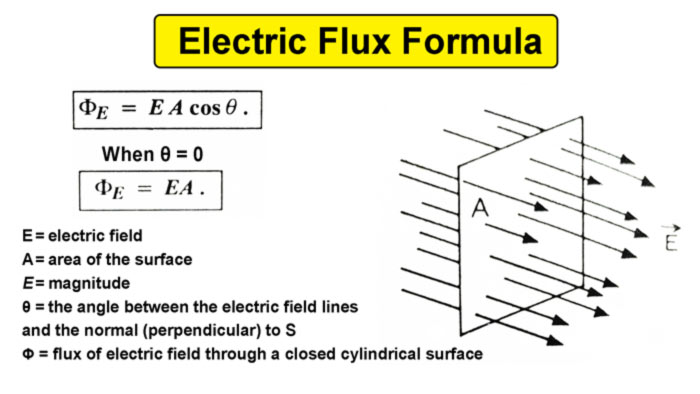
but
If the plane surface electric area is normal to E i.e. θ = 0 then
Unit and Dimensions of Electric Flux
by definition,
Where the general meaning of symbols is –
Electric Flux unit = volt – meter (Vm)
Dimensions of electric flux = [ML3T-3A-1]
Electric flux (ΦE) is a scalar quantity.
Gauss theorem or Gauss law :
In the Gauss theorem electrostatics, the relation between the electric flux passing through an imaginary closed surface and the total charge bounded by the surface. according to this
The electric flux ΦE passing through a bonded surface is 1 / Ɛ0 times the total charge q enclosed by that surface.
Here Ɛ0 permittivity of free space
E = Electric flux through a closed surface S enclosing any volume V
Q = Total charge enclosed within V
E = Electric constant
This is the integral form of Gauss’s law.

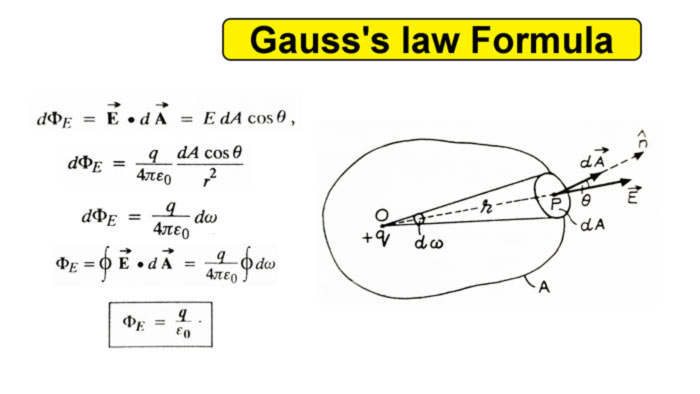
Gauss law equation : Let a point charge +Q be located at point O inside a closed surface A. Let there be a small area element dA around a point P on this page. Let OP = r
The area element dA can be represented by the vector dA drawn normal to the surface.

where is the angle θ between the vectors E and dA.
We know that E =
but
This is Gauss law.
If several point charges + q1 , + q2 , + q3 , + q4 , etc. are located inside a closed surface A, then the total electric flux passing through the surface will be equal to the algebraic sum of the electric fluxs due to all the point-charges. Due to positive charges the flux will be directed outwards and due to negative charges will be directed inwards.
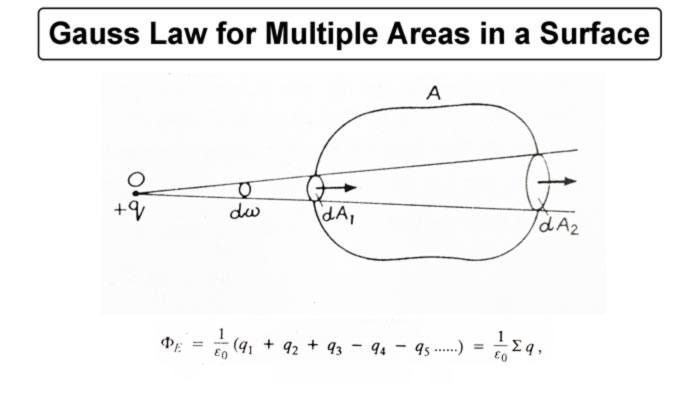
where Σq is the algebraic sum of all charges inside the closed surface.
If the point charge +q is located at point O outside the closed surface A, then the total flux passing through the surface A will be zero. The cone drawn with O as the top cuts a small area dA1 while entering the surface and cuts a small area dA2 while leaving the surface.
The flux [(q/4πƐ0)qdw] passing through dA1 is directed inwards, and the same flux [(q/4πƐ0)qdw] passing through dA2 is directed outwards.
Hence their sum is zero. This is true for all cones drawn from O on surface A. So the total electric flux for the whole page A is Zero.
Gauss law is very useful in finding the electric area due to a system of charges or a symmetrical continuous distribution of charges.